Alberto Durero (1471-1528) fue un pintor y grabador. Fue uno de los más grandes artistas del Renacimiento en el Norte de Europa. Viajó a Italia donde conoció a Jacobo de Barbari y apreció los trabajos de Luca Pacioli. Fue un gran admirador de Leonardo da Vinci. Aprendió de Barbari mucho sobre los nuevos desarrollos en perspectiva y la teoría de los proporciones. (Sobre el interés de Durero en las transformaciones matemáticas podemos ver Durero y las transformaciones de caras).
Durero estudió Matemáticas y dominó la perpectiva a través de sus estudios de Geometría. Leyó y recomendó el estudio de Euclides. Pensaba que el estudio de Geometría era indispensable para el estudio de las Artes.
En 1525 Durero publicó el primer libro de Matemáticas en alemán, los "Cuatro libros de la Medida" o "Curso en el Arte de la Medida con regla y compás". (Underweysung der Messung mit dem Zirckel und Richtscheyt). En este libro escribó sobre muchas curvas y cómo dibujar algunos polígonos. Consideró las pirámides, cilindros y otros sólidos, relojes de sol y otros instrumentos astronómicos. Estudió los cinco sólidos platónicos y algunos de los arquimedianos y dibujó desarrollos planos de estos poliedros. Introdujo la teoría de la perspectiva y describió varios aparatos para dibujar objetos desde un punto de vista determinado.
En su libro "The Life and Art of Albrecht Dürer", Panofsky destaca la importancia del trabajo de Durero: "Aparte de sus invenciones técnicas, Durero no aportó nada a la ciencia de la perspectiva tal como fue desarrollada por los italianos. Pero las secciones de su 'Unterweisung der Messung' son memorables en dos aspectos. En primer lugar, es el primer documento literario en el cual el problema de representar objetos recibe un tratamiento estrictamente científico por parte de alguien del norte de Europa; ninguno de los precursores de Durero y pocos de sus contemporáneos tuvieron una comprensión del hecho de que las reglas de la construcción de un dibujo en perspectiva estaban basadas en el concepto euclidiano de la pirámide o cono visual (...). En segundo lugar, enfatizó (...) que la perspectiva no es una discipina destinada a permanecer subsidiaria de la pintura o la arquitectura, sino que era una importante rama de las Matemáticas, capaz de ser desarrollada en lo que ahora conocemos como geometría proyectiva." (Erwin Panofsky, The Life and Art of Albrecht Dürer, p. 253).
"El 'Unterweisung' es fundamentalmente un libro para uso práctico y no un tratado de matemáticas puras. Durero quería ser entendido por artistas y artesanos" .(Erwin Panofsky, The Life and Art of Albrecht Dürer, p. 254). Su principal interés fue la aplicabilidad de técnicas geométricas por los artistas y artesanos.
Uno de los hechos más interesantes del Primer Libro es que nos presenta la primera discursión en Alemán de las secciones cónicas.
Los matemáticos griegos mostraron mucho interés en las secciones cónicas (Archimedes, Apollonius of Perga, ...), y, en particular en las que tratamos en esta página, las elipses. En matematicasVisuales ya hemos tratado en varias ocasiones las elipses.
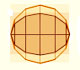
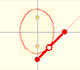
Una elipse se puede definir como el lugar geométrico de los puntos P tales que la suma de las distancias desde P a dos puntos fijos F1 y F2 (llamados focos) es constante. Usaremos esta definición más adelante.
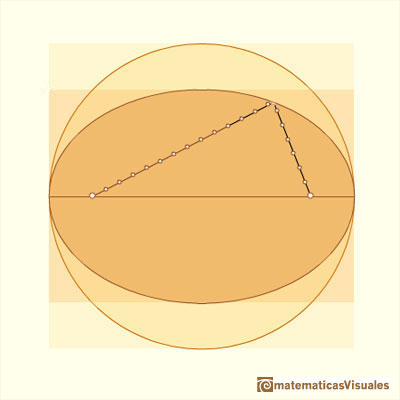
Sabemos cómo calcular el área de una elipse:

Incluso cómo construir aparatos para dibujar elipses:
Las elipses son muy importantes para los pintores porque saben que cualquier circunferencia parece una elipse cuando la vemos desde un punto de vista oblicuo.
Como un ejemplo, podemos ver varios fragmentos de pinturas con elipses que podemos admirar en el Museo Thyssen-Bornemisza en Madrid.
El modo en el que Durero trata el tema de las secciones cónicas fue original. "En vez de investigar las propiedades matemáticas de la parábola, la hipérbola y la elipse, trató de construirlas como habia tratado de constuir las espirales y epicicloides; y lo consiguió con una ingeniosa aplicación de un método familiar para arquitectos y carpinteros, pero que no se había usado antes para solucionar un problema puramente matemático, el método de la proyección paralela. Representó el cono, truncado según correspondiera, en alzado y en planta y fue transfiriendo un número suficiente de puntos de una a otra representación." (Erwin Panofsky, The Life and Art of Albrecht Dürer, p. 254-255).
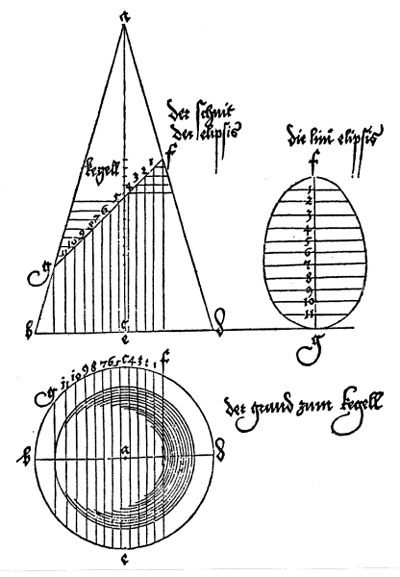
Para dibujar una elipse empezamos dibujando el eje mayor de la elipse:
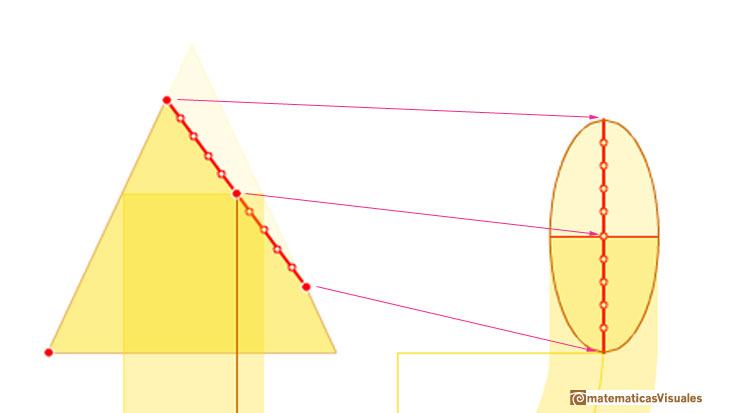
Veamos algunos ejemplos para familiarizarnos con el procedimiento.
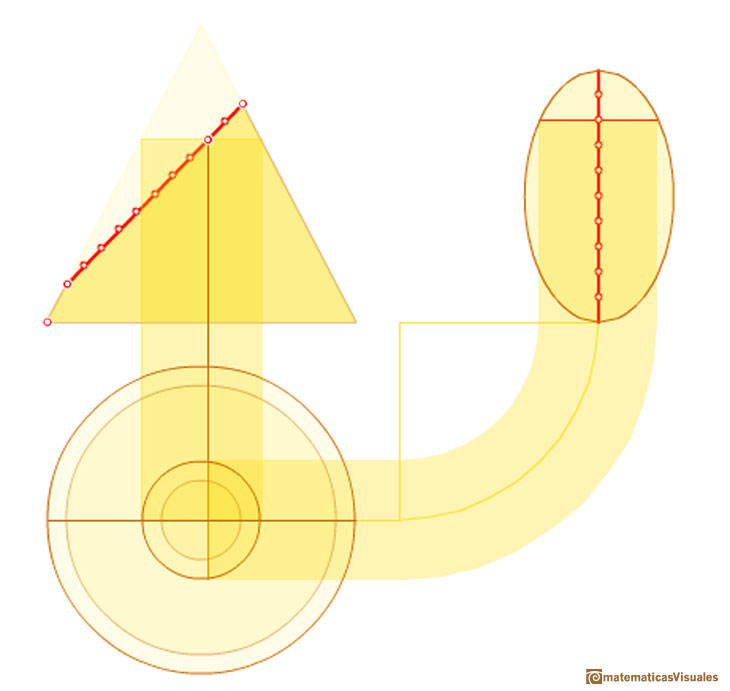
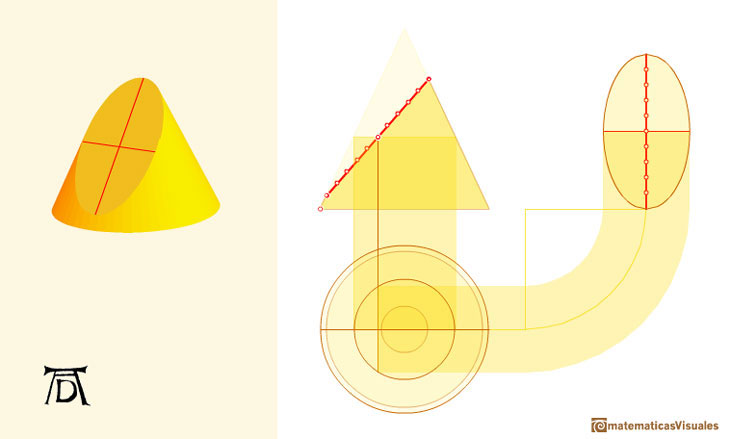
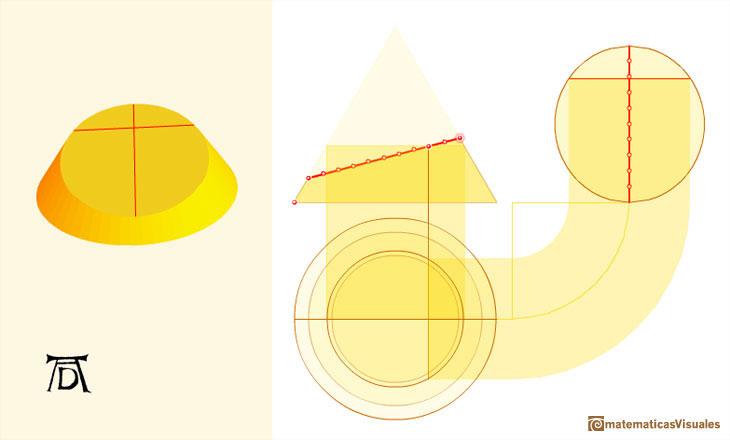
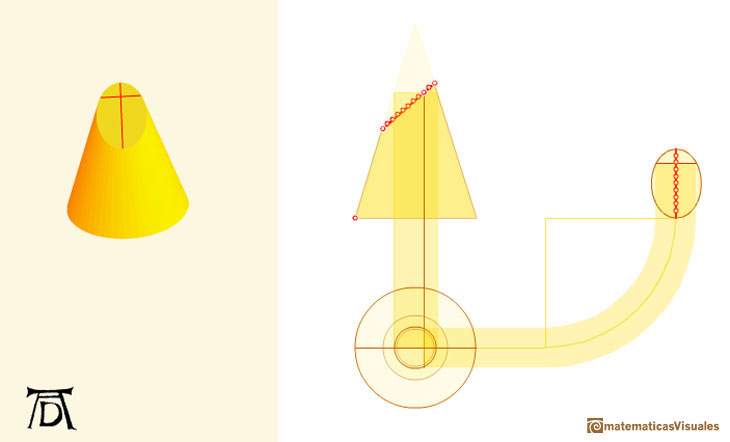
Una circunferencia es un caso particular de elipse:
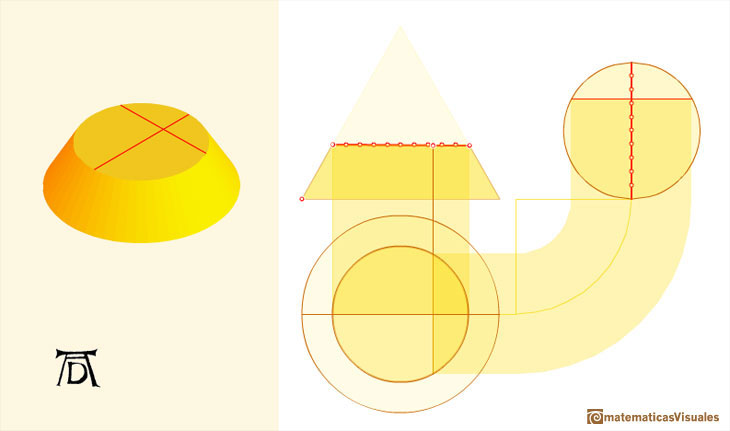
"Aunque nos parezca rudimentario, este método, que podemos llamar genético en oposición a un método descriptivo, anuncia, de alguna manera, los procedimientos de la geometría analítica y desde luego que atrajo la atención de Kepler quién, con una sonrisa, se refirió al único error en el análisis de Durero. Al igual que cualquier escolar, Durero encontró muy difícil imaginarse que una elipse es una forma perfectamente simétrica. No fue capaz de desprenderse de la idea de que debe ser más ancha conforme se ensancha el cono y, sin querer, forzó la construcción de modo que resultó una 'Eierlinie' ('línea en forma de huevo'), más estrecha por arriba que por abajo. Incluso con los métodos primitivos de Durero el error se hubiera podido evitar con facilidad. Pero el que fuera cometido no solo nos muestra un claro conflicto entre el pensamiento geométrico abstracto y la imaginación visual, sino que también prueba la independencia de Durero en sus investigaciones." (Erwin Panofsky, The Life and Art of Albrecht Dürer, p. 255).
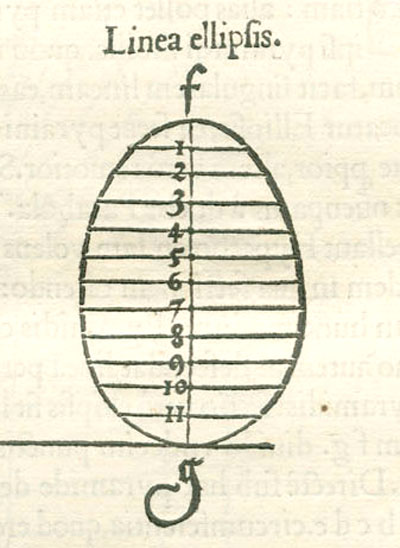
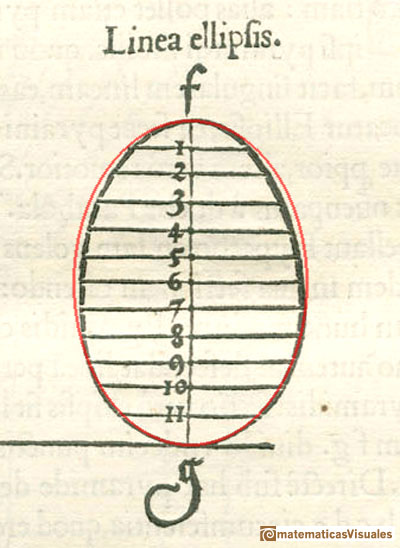
INVESTIGA
Si nos planteamos la forma que tiene una sección de un cono por un plano que pasa muy cerca del vértice, donde el cono es estrecho y muy cerca de la base, donde el cono se hace más ancho, sin prejuicios, no es fácil afirmar que la figura que va a resultar es simétrica. La intuición nos dice que la figura va a tener forma de huevo. Sabemos que no es así. Incluso alguien puede sonreir ante el error. Pero, antes o después de sonreir, ¿sabríamos probar, usando solo Matemáticas elementales, que la elipse, la sección de un cono, tiene dos ejes de simetría?
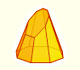
Siguiendo con la idea de que las aplicaciones interactivas nos ayudan mucho a ver las ideas matemáticas pero mucho más nos ayuda un modelo real que podamos manipular he hecho la siguiente construcción usando boles semiesféricos, imanes, una bola de acero, plástico y metracrilato. Los desarrollos de las diferentes partes del cono están dibujados sobre cartulina:







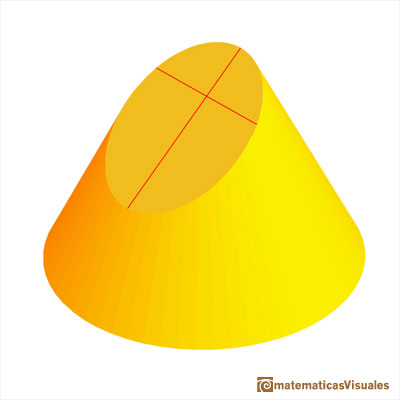
Una demostración muy visual, sencilla e interesante de que la sección de un cono por un plano que corte todas las generatrices es una elipse se le ocurrió a un matemático e ingeniero belga llamado Germinal Pierre Dandelin. Usa dos esferas que llamamos esferas de Dandelin
La demostración se puede ver en libros como 'Cálculo' de Tom Apostol quién se refiere a esta idea como la 'demostración del cono de helado'.
Aquí vamos a seguir el libro de Stanley Ogilvy 'Excursions in Geometry' para ver que la sección del cono verifica la definición de la elipse como lugar geométrico: los puntos de le elipse verifican que la suma de las distancias a dos puntos fijos (los focos de la elipse) es constante. La demostración es muy semejante a la que podemos hacer en el caso de un cilindro: Elipses como secciones de un cilindro: Esferas de Dandelin.
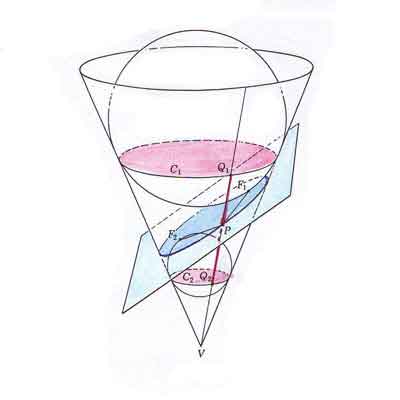
"En la figura vemos una esfera, que llamaremos esfera de Dandelin por el inventor de esta demostración, que encaja en el cono y que es también tangente a la superficie del plano 'por arriba', digamos en un punto F1. Una segunda esfera de Dandelin es tangente al cono y al plano en F2. Estos dos puntos resultarán ser los focos de la elipse.
Seleccionamos un punto P en la curva y dibujamos la recta PV. Debido a que P está en el cono, la recta PV no solo corta a las circunferencias C1 y C2, sino que también es tangente a las dos esferas, en Q1 y Q2. Pero PF1 y PF2 también son rectas tangentes a las esferas pues están en el plano tangente. Ahora bien, las tangentes a una esfera desde un punto exterior son iguales. Es decir,
Sumando,
Ahora, consideremos que P se mueve alrededor de la elipse. Habrá un nuevo Q1 y un nuevo Q2 por cada posición de P, pero la longitud Q1Q2 permanece constante (¿Por qué?). Entonces
que es la definición de una elipse con focos en F1 y F2.
Una pelota descansa en el suelo, iluminada por una sola luz eléctrica. ¿Cuál es la forma de la sombra de la bola en el suelo? ¿Dónde toca la bola al suelo?" (Ogilvy, "Excursions in Geometry", p. 80-81).




REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES