Ya hemos visto que dos puntos determinan una recta. Como función, su fórmula es un polinomio de grado menor o igual que 1.

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.
En esta página vamos a estudiar funciones que pasan por tres puntos.
Tres puntos no alineados (y que tengan distintos valores de x) determinan una función polinómica de grado 2 (que también llamamos función cuadrática).
Tiene una expresión del tipo (forma estándar):
La obtención de estas funciones cuadráticas son un caso particular de lo que llamamos Polinomios de Lagrange.
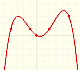
Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.
La gráfica de una función cuadrática es una parábola. Las parábolas son secciones cónicas (al igual que las elipses y las hipérbolas).
Tienen forma de copa, abierta 'hacia arriba' o 'hacia abajo'. Si consideramos valores de x muy grandes en valor absoluto, tanto positivos como
negativos resultará que los valores que toma la y también serán grandes y tendrán el mismo signo. Esto es debido a que el exponente de
mayor grado es par y depende del signo de su coeficiente, que hemos llamado a.
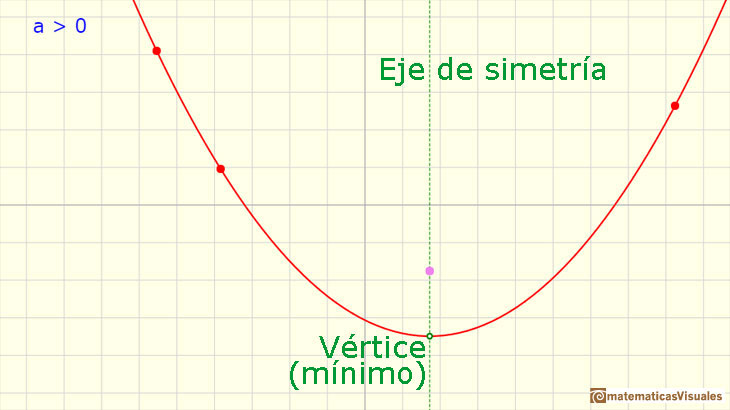
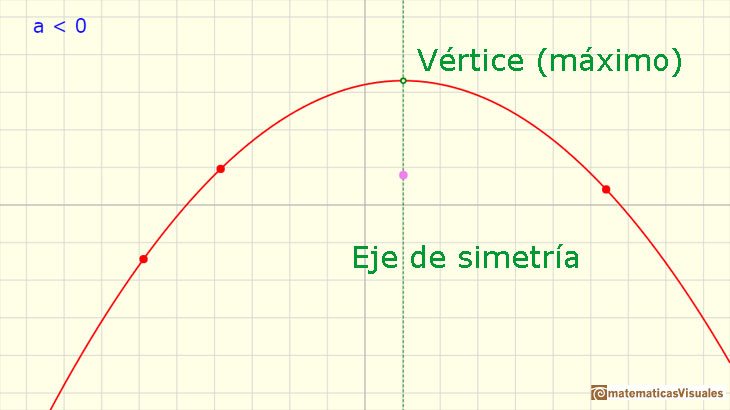
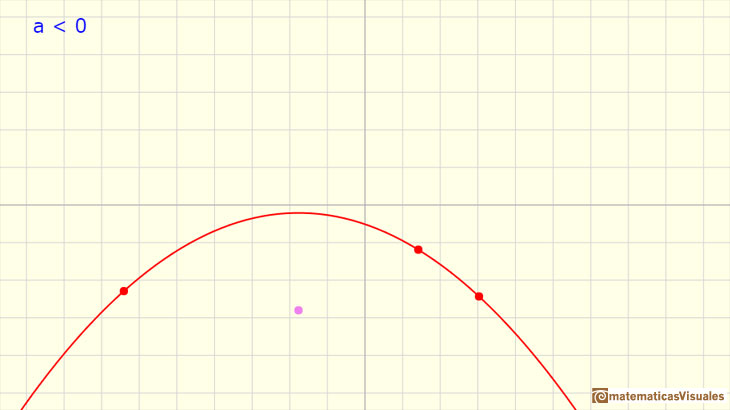
Si a es positivo la parábola se abre hacia arriba. Si a es negativo la parábola se abre hacia abajo.
INVESTIGA
Marcando la casilla 'Aux' de la aplicación interactiva se puede ver la fórmula cuadrática en la esquina superior izquierda.
Modifica los puntos rojos para mostrar diferentes parábolas y comprobar cómo el signo de a determina si la parábola se abre hacia arriba o hacia abajo.
Además, a también nos indica lo 'cerrada' que está la parábola. Cuando mayor es el valor absoluto de a más cerrada resulta la curva.
El punto violeta es importante y se llama foco de la parábola. En esta página no vamos a hablar más del foco aunque tiene mucho interés.
Aquí solo nos va a servir para moverlo
hacia arriba y hacia abajo. Haciendo esto trasladamos la parábola verticalmente sin cambiar su forma. Notaremos que solo cambia el termino independiente
c (el número que 'no lleva x'). Este número recibe a veces el nombre de 'ordenada en el origen' (un poco anticuado) y nos señala dónde la parábola
corta al eje vertical. Este punto es el más fácil de calcular: (0,c).
La parábola tiene un punto muy especial. Se trata de 'la cumbre de la montaña' o 'el fondo del valle' dependiendo de si la parábola se abre hacia
arriba o hacia abajo. Se trata de un máximo o de un mínimo de la función
La parábola tendrá un máximo si el coeficiente a es un número negativo y tendrá un mínimo si ese coeficiente es
positivo). Este punto se llama vértice de la parábola.
También notamos que la parábola es simétrica respecto de una recta vertical. Esta recta vertical pasa por el vértice y se llama
eje de simetría de la parábola. Al final de la página aprenderemos a hallarlos.
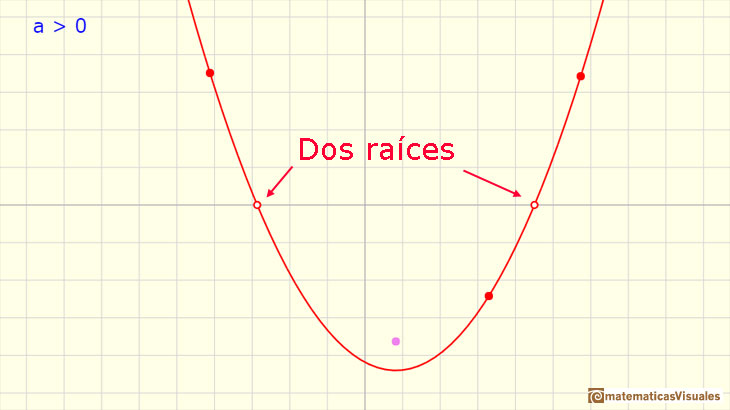
Ahora vamos a estudiar los posibles puntos de corte con el eje de las X. Este asunto está relacionado con la resolución de una ecuación cuadrática.
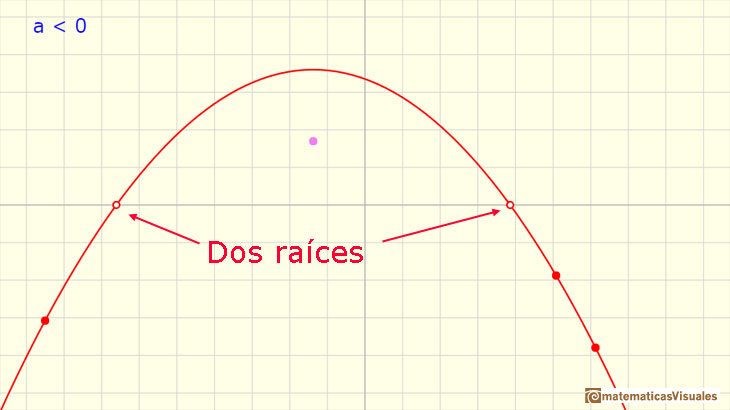
Algunas parábolas cortan al eje de las X (eje de abcisas) en dos puntos. Esos valores son las raíces (reales) o ceros del polinomio.
Podemos obtener esas raíces resolviendo una ecuación cuadrática:
Las soluciones de una ecuación cuadrática vienen dadas por:
El discriminante se define como:
Si el discriminante es mayor que 0, la ecuación cuadrática tiene dos raíces reales, x1, x2. En este caso, podemos
escribir la función cuadrática descompuesta en sus factores de esta manera:
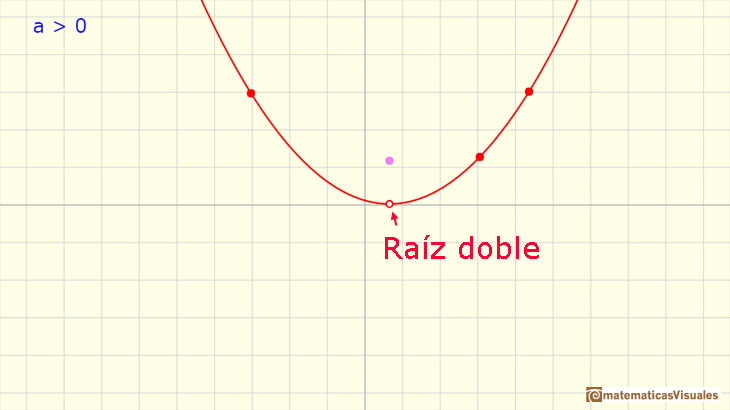
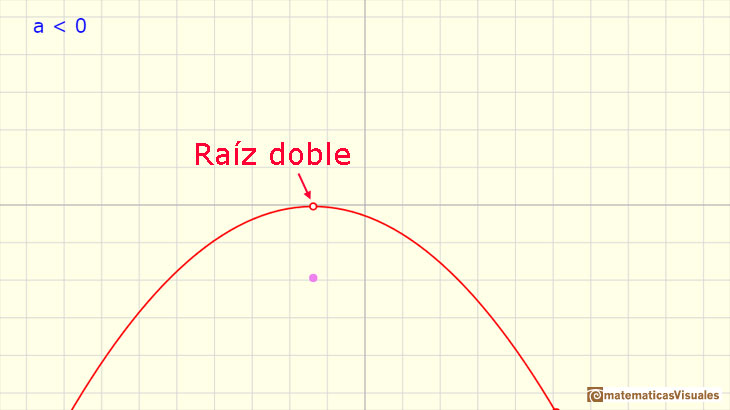
Algunas parábolas solo tocan al eje de abcisas en un solo punto.
Esto ocurre cuando el discriminante es igual a cero y la solución de la ecuación cuadrática es:
En este caso decimos que la raíz es una raíz doble. La función cuadrática se factoriza así:
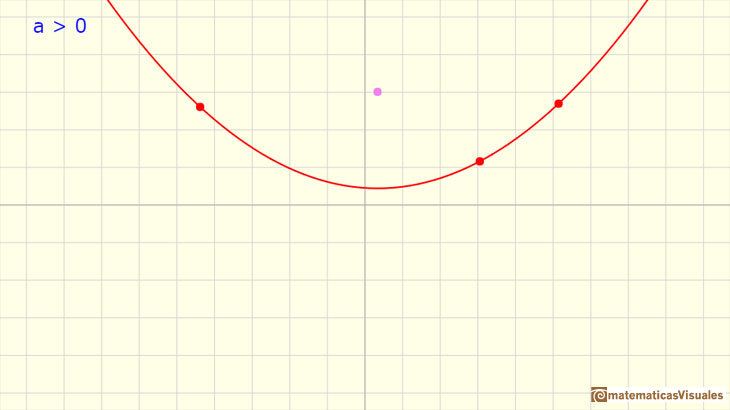
Algunas parábolas no tocan ni cortan al eje de las x. En este caso, el discriminante es menor que cero y la ecuación cuadrática no tiene
soluciones reales.
Aquí podemos ver más ejemplos de parábolas con dos raíces reales, con una sola raíz doble y sin raíces reales:
INVESTIGA
Moviendo el punto violeta trasladamos la parábola arriba y abajo. Si nos fijamos en la fórmula solo cambia le valor del término independiente c.
Si partimos de una parábola con dos puntos de corte, al trasladar la parábola arriba y abajo podemos ver como los puntos de corte se alejan o se acercan hasta
confundirse en uno solo (raíz doble) o desaparecer (no raíz real).
Para terminar, volvemos al vértice y al eje de simetría de la parábola. El eje de simetría tiene que pasar por el vértice y si la parábola corta al eje de
las X en dos puntos el eje tiene que pasar por el medio de esas dos soluciones de la ecuación.
La ecuación del eje de simetría de la parábola es:
El vértice de la parábola tiene coordenadas:
Las parábolas son secciones cónicas. Se genera una parábola al cortar un cono por un plano paralelo a una generatriz. Así podemos ver una parábola usando
un matraz apoyado sobre una superficie:
Las funciones cuadráticas con coeficientes reales o complejos tienen siempre dos raíces (reales o complejas)(Teorema fundamental del Álgebra):
REFERENCIAS
Michael Spivak, 'Calculus', Third Edition, Publish-or-Perish, Inc.
Tom M. Apostol, 'Calculus', Second Edition, John Willey and Sons, Inc.
I.M. Gelfand, E.G. Glagoleva, E.E. Shnol, 'Functions and Graphs', Dover Publications, Mineola, N.Y.
 SIGUIENTE
SIGUIENTE
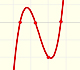
Las funciones cúbicas son polinomios de grado 3. Una función cúbica real siempre corta al eje de abcisas por lo menos una vez.
 ANTERIOR
ANTERIOR
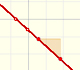
Dos puntos determinan una línea recta. Como función son las funciones afines. Estudiaremos la pendiente de la recta y como podemos obtener la ecuación de la recta que pasa por dos puntos. Estudiaremos el corte con el eje de abcisas.
MÁS ENLACES
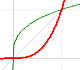
Potencias con exponente natural son funciones importantes pues son la base de los polinomios. Sus funciones inversas son las raíces que son funciones potencia con exponente racional positivo.

Se trata de encontrar el polinomio de menor grado que pasa por una serie de puntos del plano. Es un problema de interpolación que aquí resolvemos usando los polinomios de Lagrange.

La derivada de una función lineal es la función constante cuyo valor es la pendiente de la recta.
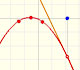
La derivada de una función cuadrática es una función afín, es decir, es una línea recta.
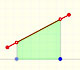
Como una introducción a las funciones lineales a trozos estudiamos el caso más sencillo, las funciones lineales restringidas a un intervalo abierto: sus gráficas son segmentos.
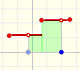
Una función constante a trozos (o función escalonada) está definida por varias subfunciones que son funciones constantes.
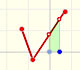
Una función continua lineal a trozos se define con varios segmentos o rayos que están unidos de un modo continuo, sin saltos entre ellos.
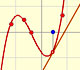
La derivada de una función cúbica es una función cuadráticas, es decir, una parábola
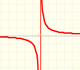
Las funciones racionales son las que pueden escribirse como cociente de dos polinomios. Las funciones racionales lineales son las más sencillas de este tipo.
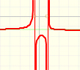
Si el denominador de una función racional es un polinomio de grado 2 la función tiene dos, una o ninguna singularidad real (asíntotas verticales y singularidades evitables).
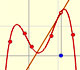
Los polinomios de Lagrange son polinomios que pasan por n puntos dados. Usamos los polinomios de Lagrange para explorar funciones polinómicas más generales y sus derivadas.
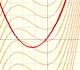
Si la derivada de F(x) es f(x) decimos que F es una antiderivada de f. También decimos que F es una primitiva o una integral indefinida de f.
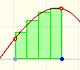
La integral formaliza el concepto intuitivo de área. Para su definición aproximamos el área usando rectángulos.

Las funciones monótonas definidas en intervalos cerrados son interables. En estos casos podemos acotar el error que cometemos al aproximar la integral usando rectángulos.
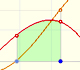
Si consideramos el límite inferior de integración fijado y podemos calcular la integral definida para diferentes valores del límite superior de integración entonces podemos definir una nueva función: una integral indefinida de f.

Es fácil calcular el área bajo una línea recta y el eje de abcisas. Es un primer ejemplo de integración que nos permite entender la idea e introducir algunos conceptos básicos: integral como área, límites de integración, áreas positivas y negativas.
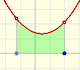
Calcular el área bajo una parábola es mucho más difícil que calcular áreas bajo una recta. Aquí mostramos como aproximar el área usando rectángulos y que una función integral de un polinomio de grado 2 es un polinomio de grado 3.
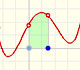
Estudiamos algunos conceptos básicos sobre integración aplicados a funciones polinómicas de cualquier grado. Las funciones integrales de funciones polinómicas son polinomios de un grado más que la función original.
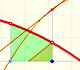
El Teorema Fundamental del Cálculo afirma que toda función continua tiene una antiderivada y nos muestra cómo construir una usando la integral.
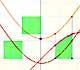
El Segundo Teorema Fundamental del Cálculo nos proporciona una herramienta muy potente para calcular integrales definidas (si conocemos una primitiva o antiderivada de la función).

Al aumentar el grado del polinomio de Taylor se aproxima a la función exponencial en un intervalo más y más amplio.
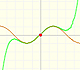
Al aumentar el grado del polinomio de Taylor se aproxima a la función seno en un intervalo más y más amplio.
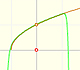
La función no está definida para valores menores que -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.

La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
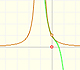
La función tiene una singularidad en -1. Los polinomios de Taylor en torno al origen aproximan la función entre -1 y 1.
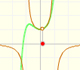
La función tiene dos singularidades reales, en -1 y en 1. Los polinomios de Taylor aproximan la función entre en un intervalo simétrico respecto al centro del desarrollo. Su radio es la distancia a la singulardidad más próxima.
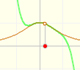
La función es continua y no tiene singularidades reales. Sin embargo, los polinomios de Taylor sólo aproximan la función en un intervalo. Entenderemos un poco mejor este comportamiento estudiando una función compleja.

Las potencias de exponente natural tienen un cero de multiplicidad n.

Un polinomio de grado 2 tiene dos raíces o ceros. En esta representación podemos ver los óvalos de Cassini y la lemniscata.

Un polinomio de grado 3 tiene tres ceros o raíces. Podemos modificar los tres ceros de este tipo de polinomios.

Un polinomio de grado n tiene n ceros o raíces.


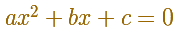


 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR














































