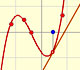
Ya hemos estudiado funciones polinómicas como las funciones constantes y de grado 1 (que se representan con rectas), de grado 2 (que se representan con parábolas) y de grado 3.
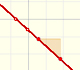
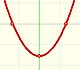
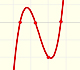
El objetivo de esta página es familiarizarnos con funciones polinómicas de mayor grado y relacionarlas con una de las técnicas de interpolación que llamamos polinomios de Lagrange.
En lo que hemos visto hasta ahora hemos partido de un conjunto de puntos distintos del plano. Estos puntos tienen que tener diferente coordenada x, esto es necesario pues queremos hablar de funciones.
Dos puntos determinan una recta (y como función polinómica se trata de un polinomio de grado 1 o quizás 0 si la recta es horizontal y entonces la función es contante), tres puntos que no estén en linea recta determinan una parábola (polinomio de grado 2), cuatro puntos en general determinan una función cúbica (polinomio de grado 3).
La idea es extender este modo de generar funciones polinómicas con más puntos para obtener polinomios de mayor grado que seguirán la regla de que 5 puntos pueden determinar un polinomio de grado 4, 6 puntos un polinomio de grado 5 y, en general, n + 1 puntos determinarán una función polinómica de grado n. Un modo de conseguir esto es usando los polinomios de interpolación de Lagrange.
Antes de tratar este asunto de los polinomios de Lagrange vamos a ver algunas propiedades sencillas de estas funciones polinómicas. Al final de la página (en el apartado D) hay una descripción más técnicas de los polinomios de Lagrange.
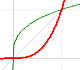
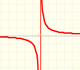
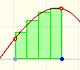
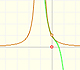
A) Nos fijamos en primer lugar en qué ocurre cuando consideramos valores de x grandes en valor absoluto (es decir, tanto positivos como negativos). Vamos a ver un par de ejemplos. Esta función está determinada por 7 puntos y se trata de un polinomio de grado 6:
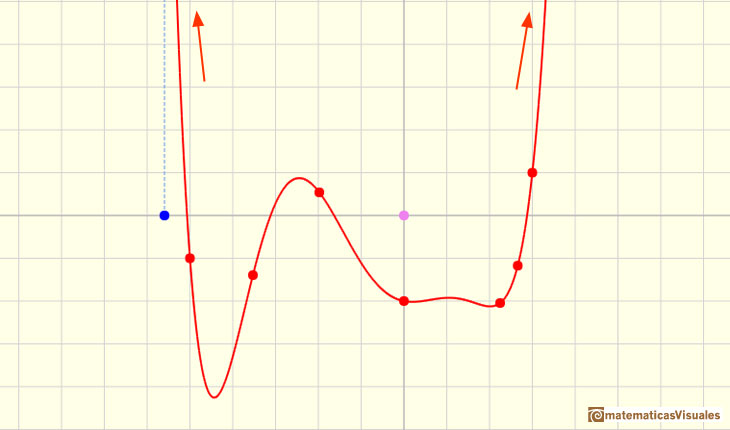
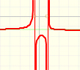
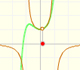
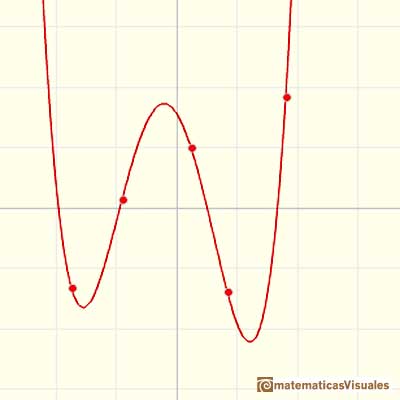
La función del siguiente ejemplo está determinada por 8 puntos y el polinomio es de grado 7:
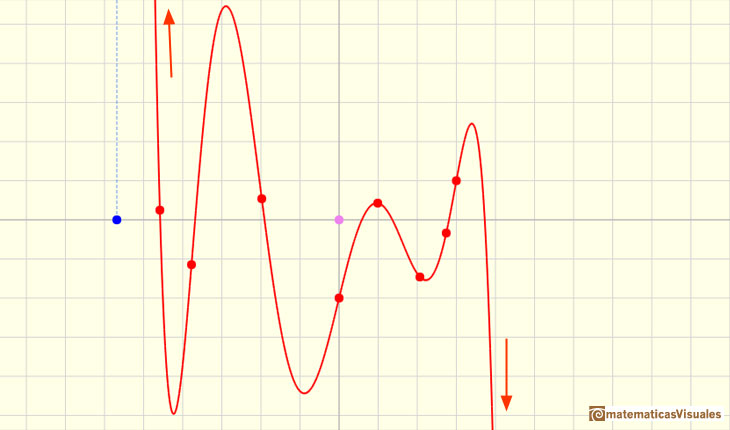
Podemos notar que cuando x es grande también es grande el valor de la función, unas veces positiva y otras negativa. También podemos ver que la función crece (o decrece) con mayor 'rapidez' conforme aumentamos el grado del polinomio.
INVESTIGA
El comportamiento de la función polinómica cuando consideramos valores de x grandes es diferente cuando el polinomio tiene grado par o impar.
¿Cómo podríamos describir esa diferencia de comportamiento en relación con la paridad del grado?
Si pensamos en que el polinomio está ordenado entonces empieza con un número (que multiplica a la x con mayor grado). A veces llamamos a este número el coeficiente director del polinomio.
¿En qué afecta el signo (positivo o negativo) del coeficiente director en la forma general de la gráfica de la función polinómica?
B) Nos vamos a fijar ahora en los puntos en los que la gráfica corta al eje de las X, el eje de abcisas.
Esos valores de x se llaman ceros de la función (son las raíces reales del polinomio o las soluciones de la ecuación P(x)=0).
Empleamos la expresión 'cero real' o 'raíz real' para referirnos a que son números del conjunto de los Números Reales y para distinguirlos de los 'ceros complejos' que pueden existir y que entonces son números que pertenecen al conjunto de los Números Complejos. Este conjunto de números se estudia más adelante. Aquí solo estamos en el mundo de los Números Reales. Los ceros reales son los que se corresponden con puntos de corte con el eje de las X y son los que ahora estamos estudiando.
Marcando la casilla 'Ceros' se marcan en rojo esos puntos de corte.
Muchas veces esos valores no son fáciles de calcular. Para hacerlo se tiene que resolver una ecuación polinómica que puede ser muy difícil de resolver si el grado es grande. De hecho, si el grado es mayor que 4 ya no hay una fórmula explícita que nos permita calcularlos. En estos casos podemos recurrir a cálculos aproximados que se pueden hacer con muchísima precisión.
INVESTIGA
Modificando el grado del polinomio explora situaciones extremas del tipo:
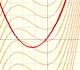
¿Se puede conseguir funciones polinómicas que no tengan ningún cero real?
¿Afecta en algo el que el polinomio tenga grado par o impar? ¿Hay funciones polinómicas de grado par sin ceros reales? ¿Y de grado impar?
Puedes ver que las funciones polinómicas de grado impar siempre tienen, por lo menos, un cero real. ¿Sabrías dar una explicación intuitiva de este hecho usando lo que hemos visto en el apartado anterior?
Para un determinado grado del polinomio ¿cuántos ceros reales puedes conseguir como máximo?
Las respuestas a las cuestiones anteriores nos las da un teorema muy importante: el Teorema Fundamental del Álgebra. Este teorema afirma que cualquier función polinómica tienen tantos ceros como su grado. Por ejemplo, si es de grado 5 tendrá 5 ceros. Pero estos ceros pueden ser reales o complejos.
Si pensamos solo en los ceros reales podemos decir que una función polinómica tiene, como mucho, tantos ceros como su grado. Nunca más,
Si tiene menos ceros reales que su grado entonces tiene ceros complejos. Estos ceros complejos caen fuera de nuestro mundo de los números reales pero es bueno saber que van por parejas. Cuando el grado del polinomio es impar, por fuerza, uno de sus ceros va a quedar desparejado y será un cero real. (Otro modo de justificar que las funciones polinómicas de grado impar tienen, por lo menos, un cero real es el Teorema de Bolzano).
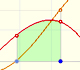
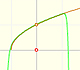
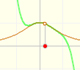
Veamos unos ejemplos. El primero es un polinomio de grado 5 con una sola raíz real:
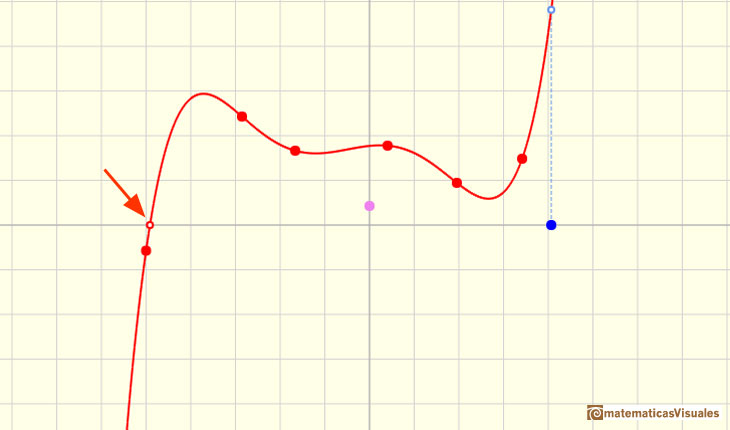
Un polinomio de grado 5 con 5 raíces reales distintas:
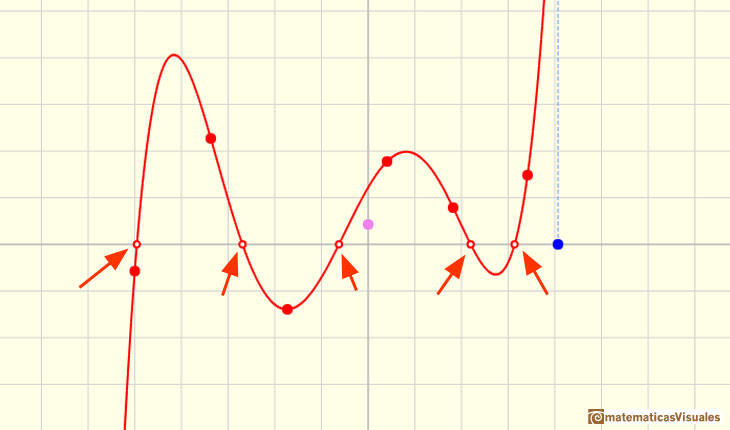
A veces estos ceros están repetidos y entonces los contamos dos, tres o más veces. Decimos que son ceros dobles, ceros triples ....
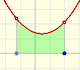
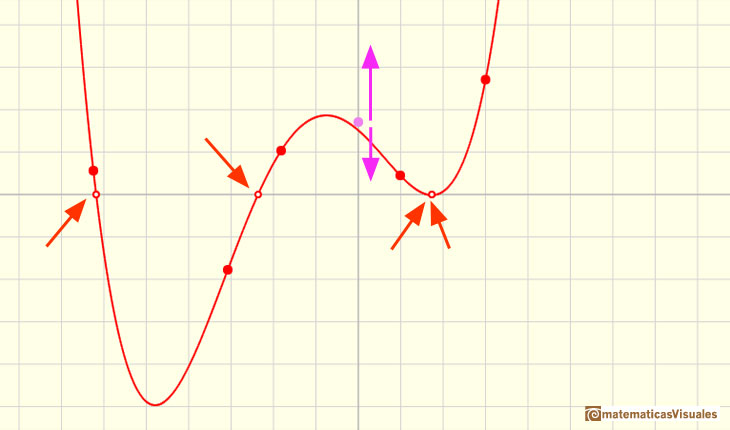
El siguiente ejemplo es un polinomio de grado 4 con 4 raíces reales, una de ellas es un cero doble:
INVESTIGA
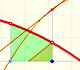
Moviendo el punto violeta verticalmente trasladamos la gráfica de la función arriba y abajo. No modificamos la forma de la función pero sí que cambiamos los puntos de corte con el eje de las x.
Si lo haces con cuidado podrás ver cómo dos ceros se aproximan hasta confundirse en uno solo. Ese es un motivo por el que decimos que el cero es doble.
INVESTIGA LA RELACIÓN CON EL ÁLGEBRA
Aquí estamos estudiando las funciones polinómicas y sus gráficas. Este estudio corresponde al área de las Matemáticas que llamamos Análisis.
Los polinomios son también un objeto de estudio importantísimo del Álgebra.
Uno de sus intereses es la factorización de polinomios (o descomposición de un polinomio en factores). Los ceros de un polinomio están directamente relacionados con los factores en los que descomponemos un polinomio.
Si has estudiado este asunto probablemente podrás contestar estas preguntas:
Un polinomio de grado 2 tiene 2 raíces reales distintas (en este caso, además, sabemos calcularlas). ¿Qué podemos decir de su descomposición factorial?
Si un polinomio de grado 2 solo tiene una raíz real doble. ¿Qué nos ha pasado al intentar encontrar las raíces de la ecuación? ¿Cómo es su descomposición factorial?. En un caso así decimos que hay una 'identidad notable'.
Una función polinómica de grado 2 no tiene ningún cero real, no corta al eje de abcisas en ningún punto. ¿Qué nos ha ocurrido al intentar resolver la ecuación de segundo grado? ¿Podemos descomponer ese polinomio en el mundo de los Números Reales?
Si sabemos que un polinomio de grado 4 tiene 4 raíces reales distintas ¿qué podemos decir de su descomposición factorial?
Si un polinomio de grado 3 tiene dos raíces reales distintas, una de ellas doble ¿cómo será su descomposición factorial?
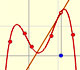
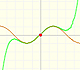
C) En tercer lugar vamos a ver otra propiedad general de las funciones polinómicas. Solo un poco por encima pues es un asunto en el que profundizaremos más adelante, cuando estudiemos las derivadas. Muchas funciones polinómicas tienen 'montañas' y 'valles' (o 'subidas' y 'bajadas'). De esto trata el análisis del crecimiento y decrecimiento de una función. Si tiene una montaña o un valle entonces tendrá una 'cumbre de la montaña' o 'el fondo de un valle'. Son los llamados máximos y mínimos locales o relativos de una función.
Si intentamos hacer un estudio del crecimiento y decrecimiento de una función polinómica y de sus máximos y mínimos locales sin la ayuda de las derivadas los resultados no pueden ser muy precisos. Pero pensando en ello nos vamos familiarizando con la terminología que nos será útil más adelante.
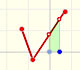
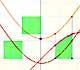
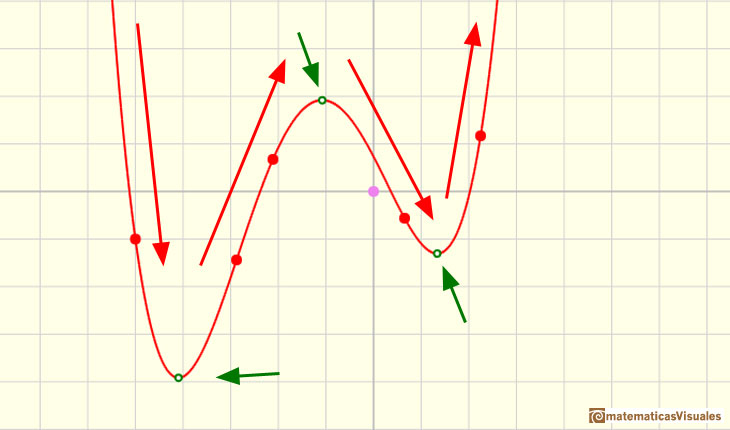
Los máximos y mínimos están entre los llamados puntos críticos. Estos puntos se muestran en verde cuando se marca la casilla 'Critic.' en la aplicación interactiva.
INVESTIGA
Parece haber una relación entre el número de montañas y valles de una función polinómica y su grado.
Por ejemplo, con cinco puntos generamos una función polinómica de grado 4. ¿Podemos hacer que tenga 4 montañas y valles?
¿Cuál es el número máximo de montañas y valles que puede tener una función polinómica en relación con su grado? Atrévete a hacer una hipótesis.
Modificando los puntos rojos podemos ver cómo, en algunos casos, los puntos verdes se aproximan y se confunden en uno solo (como ocurría con los ceros dobles).
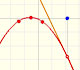
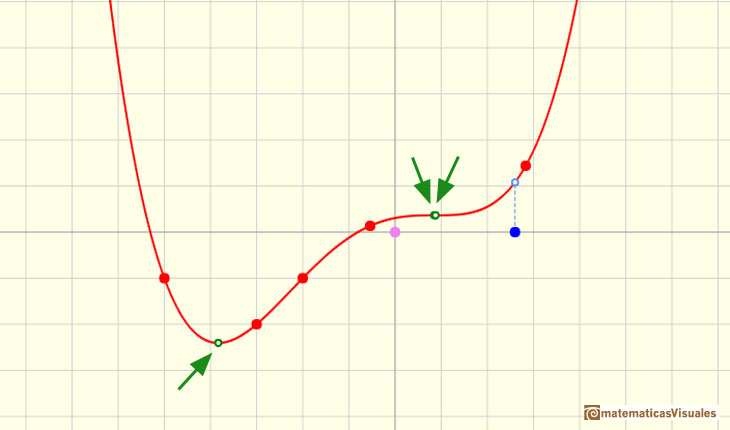
Intenta generar algún caso de este tipo. A veces el punto crítico (verde) resulta que no es un máximo o mínimo local de la función.
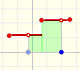
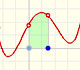
En el siguiente ejemplo hay un punto crítico 'doble' que no es máximo ni mínimo local de la función
D) Vamos a hacer ahora una descripción más técnica y complicada de cómo se construyen los polinomios de Lagrange.
Empezamos con un conjunto de n + 1 puntos en el plano (que tengan diferentes coordenadas x):
(x0, y0), (x1, y1), (x2, y2),....,(xn, yn).
Nuestro objetivo es encontrar una función polinómica que pase por esos n + 1 puntos y que tengan el menor grado posible. Un polinomio que pase por varios puntos determinados se llama un polinomio de interpolación.
Vamos a ver una forma de la solución que es el llamado polinomio de interpolación de Lagrange. (Lagrange publicó su fórmula en 1795 pero ya había sido publicada en 1779 por Waring y redescubierta por Euler en 1783).
La fórmula general para el polinomio de interpolación de Lagrange es
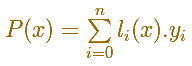
Donde usamos polinomios básicos de Lagrange:
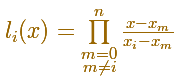
Expandiendo el producto para verlo mejor:
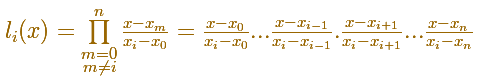
Estos polinomios básicos de Lagrange se construyen con una propiedad:
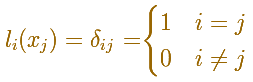
Entonces es muy fácil comprobar que estos polinomios pasan por todos los n+1 puntos dados (es decir, es un polinomio de interpolación):
El grado del polinomio de interpolación de Lagrange es igual o menor que n. Es el menor grado posible. El polinomio encontrado es único. Hay otras maneras de calcular este polinomio (con sus ventajas e inconvenientes). La forma de Lagrange es sencilla y se comprueba con facilidad que es un polinomio de interpolación y su grado. Pero para conocer los coeficientes del polinomio hay que simplificar los términos. Otra característica de esta forma de encontrar el polinomio es que si añadimos o quitamos puntos hay que recalcularlo otra vez.
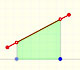
Vamos a repasar algunos ejemplos. El más sencillo es una recta. Dados dos puntos (x0, y0) y (x1, y1) hay exactamente una recta que pasa por esos dos puntos:
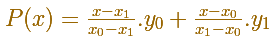
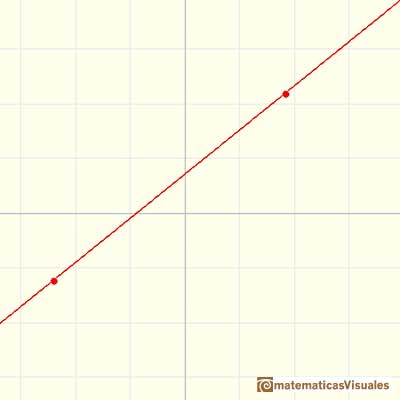
Dados tres puntos (x0, y0), (x1, y1) y (x2, y2), con coordenadas x diferentes, o bien los tres puntos están en una recta o hay un polinomio de segundo grado (una parábola) que pasa por esos tres puntos. En cualquier caso, hay un polinomio de grado como mucho 2 que pasa por esos tres puntos.
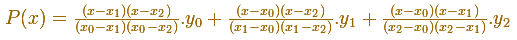
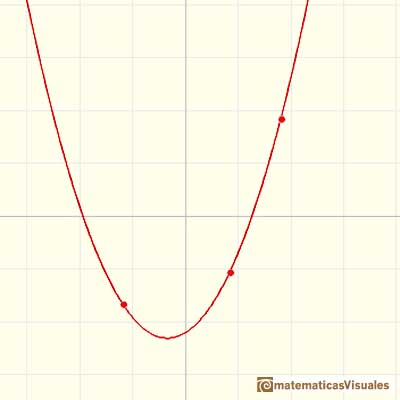
Si tenemos 4 puntos, podemos encontrar un polinomio de grado 3 (o quizás una parábola o una línea recta en algunos casos) que pasa por esos 4 puntos:
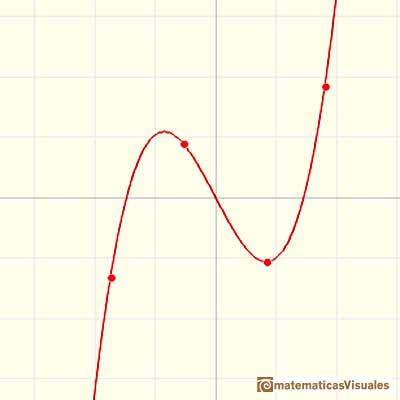
Un función polinómica de grado 4 pasa a través de 5 puntos:
Usaremos los polinomios de interpolación de Lagrange para construir aplicaciones interactivas relacionadas con funciones polinómicas, sus derivadas e integrales.
Las funciones polinómicas con coeficientes reales o complejos de grado n tienen siempre n raíces (reales o complejas)(Teorema fundamental del Álgebra):
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES