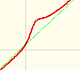
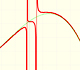
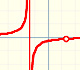
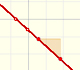
Una función racional es una función que puede escribirse como cociente de dos polinomios.
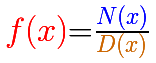
Si el denominador es un número (un polinomio de grado 0), entonces la función es un polinomio. Por lo tanto, las funciones polinómicas son funciones racionales. En estas páginas sobre funciones racionales vamos a considerar solamente funciones racionales cuyo denominador es un polinomio de grado mayor que 0.
Esta serie sobre funciones racionales se complementa con una nueva serie en la que se destaca el estudio de la continuidad, asíntotas verticales y discontinuidades evitables.
Las funciones racionales pueden tener características que las diferencian de las funciones polinómicas y que vamos a revisar en estas páginas:
- Singularidades: En algunos casos, algunos valores de x son problemáticos. Esto es debido a que las funciones racionales hay un denominador que puede ser 0 y no podemos dividir entre 0. Esos valores de x que hacen 0 el denominador juegan un papel especial. Como no podemos calcular el valor de la función en esos valores decimos que la función no está definida para esos valores de x.
También decimos que esos puntos no pertenecen al dominio de la función. El dominio de una función racional está determinado por las restricciones impuestas por el denominador: dividir entre 0 es imposible.
El dominio es el conjunto de los números reales para los que la función está definida. En el caso de las funciones racionales es el conjunto de todos los números reales que no son ceros del denominador. Por lo tanto, para determinar el dominio de una función racional tenemos que encontrar los ceros reales del denominador.
A estos puntos se les llama singularidades y es interesante ver cómo se comporta la función cerca de esos puntos.
- Continuidad: Las funciones racionales son continuas en su dominio (pero su dominio puede no ser todos los números reales).
- Comportamiento "en el infinito": Es interesante el estudio del comportamiento de la función cuando x se hace más y más grande en valor absoluto (siendo x positivo o negativo). Veremos que en algunos casos la función se aproxima a una recta (horizontal u oblicua). En estos casos diremos que la función tiene una asíntota horizontal u oblicua (según los casos). En todos los casos el comportamiento de una función racional "en el infinito" está determinado por una función polinómica.
Empezamos nuestro estudio con las funciones racionales lineales. Una función racional lineal es una función racional cuyo numerador es un número o un polinomio de grado 1 y que tiene por denominador un polinomio de grado 1.
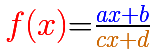
Vamos a repasar un poco de la terminología que usamos cuando hablamos de la singularidad de una función racional lineal pues tratamos la misma idea desde diferentes puntos de vista.
Cuando queremos estudiar una función lo primero que solemos querer saber es para qué valores de la variable independiente x podemos conocer el valor de la función. Ese conjunto de números reales se llama DOMINIO de la función.
Si la función viene dada por una fórmula y en esa fórmula hay una división (como ocurre en el caso de las funciones racionales) nos tenemos que plantear si para algún valor de la x el denominador vale 0 y estamos intentando dividir entre 0 () pues eso no lo podemos hacer.
Entonces decimos que ese valor de x NO PERTENECE AL DOMINIO de la función.
Para las funciones racionales lineales siempre podremos encontrar un solo valor al que le ocurre esto. Otras funciones racionales pueden tener uno o varios de esos valores o ninguno.
Para encontrar ese valor recurrimos al álgebra e intentamos resolver una ecuación (el polinomio de grado 1 del denominador = 0). El valor que encontramos en este caso es la SOLUCIÓN de la ecuación y también recibe el nombre de CERO del polinomio o RAÍZ del polinomio.
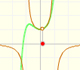
Este polinomio de grado 1 del denominador se puede representar gráficamente como una recta oblicua. El valor que hemos encontrado se corresponde con el PUNTO DE CORTE de la recta con el eje de las X (eje de abcisas). En la aplicación está representado por un puntito naranja.
En un primer momento la aplicación interactiva muestra la función racional más simple. En la aplicación vemos una recta de color naranja que es el polinomio del denominador de la función racional. El valor de la coordenada y del punto azul representa el número que está en el numerador. Más adelante veremos cómo al modificar la recta y el valor que representa el punto azul cambia la gráfica de la función. En un primer momento, no modificaremos el punto verde pues más adelante explicaremos su significado.
La más simple de las funciones racionales es
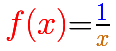
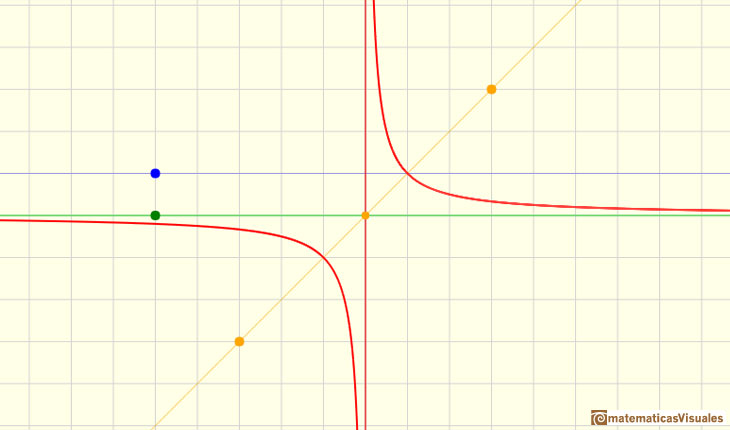
Al dibujar su gráfica obtenemos una curva que llamamos hipérbola equilátera. Está función está relacionada con la proporcionalidad inversa.
Cuando x=0 no podemos calcular el valor de la función porque no podemos dividir entre 0 (abusando del lenguaje, a veces se dice que 'el cociente se hace infinito'). La función no está definida en x=0. Es decir, el dominio de la función es:
Para x = 1 resulta y = 1. Para x > 1 el numerador es más pequeño que el denominador y el cociente resulta menor que 1.
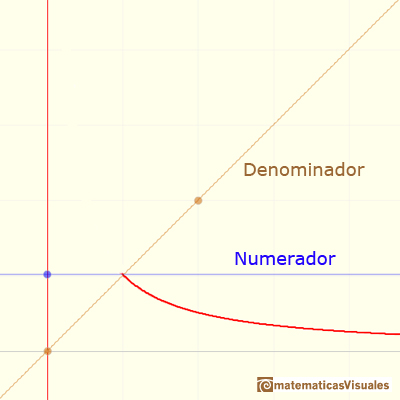
Veamos con más detalle el comportamiento de la función cuando x se hace más y más grande. Conforme aumenta x la fracción 1/x disminuye. Por lo tanto, si nos movemos desde el 0 hacia la derecha, el valor de y=1/x es cada vez menor y la curva se aproxima al eje de abcisas tanto como queramos. Es decir, la función se comporta como una recta horizontal. A esta recta la llamamos asíntota horizontal.
La recta y=b es una asíntota horizontal de la gráfica de f(x) si f(x) se aproxima a b conforme x aumenta o disminuye sin cota.
En este primer caso, la asíntota horizontal es el eje de abcisas:
El polinomio de grado 1 del denominador (en la aplicación es la recta naranja) se hace 0 para algún valor de x y ese valor no pertenece al dominio de la función.
Interesa estudiar el comportamiento de la función cuando nos acercamos a ese valor por la derecha y por la izquierda.
Vamos a verlo en el caso más sencillo de la hipérbola equilátera:
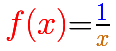
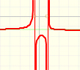
Cuando nos aproximamos a 0 por el lado del 1 (valores positivos), el denominador se está aproximando a 0 mientras que el numerador es igual a 1. La función aumenta cuanto queramos, aumenta sin límite y obtenemos una rama que se 'va hacia el infinito'.
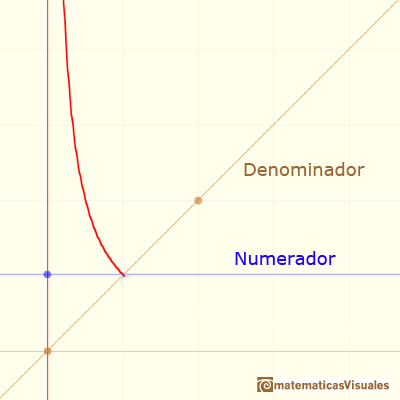
Si nos aproximamos a 0 por la izquierda (valores negativos) entonces la gráfica de la función se 'va hacia el infinito' pero negativo.
Decimos que la función tiene una asíntota vertical. La gráfica de esta función está dividida en dos 'ramas'.
La recta x=b es una asíntota vertical de la gráfica de f(x) si f(x) crece o decrece sin cota conforme x se acerca a b por la derecha o por la izquierda.
Una función racional puede tener asíntotas verticales en los ceros del denominador. Veremos más adelante que hay una situación diferente cuando el cero del numerador también sea cero del numerador.
En el caso de la hipérbola equilátera, la asíntota vertical es:
Si utilizamos la lupa podemos ver claramente las dos asíntotas de la hipérbola:
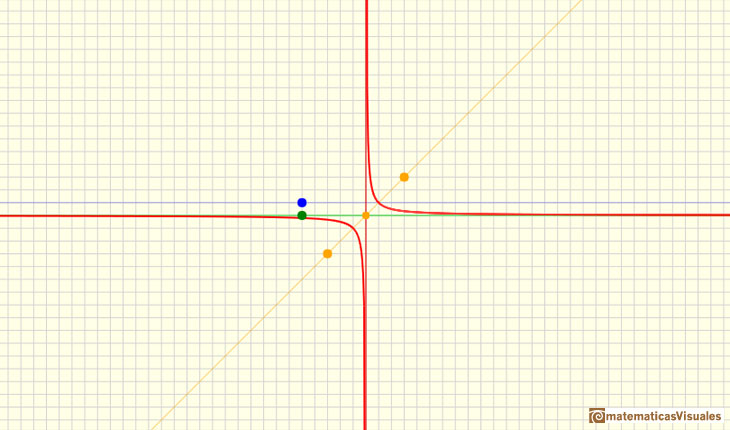
Si añadimos un número al denominador, el resultado es una traslación de la hipérbola a lo largo del eje de abcisas. En la aplicación interactiva esto se consigue moviendo la recta del denominador (naranja) usando el punto central naranja. Al modificar el punto de corte de esta recta con el eje de abcisas (el cero del denominador) se traslada a derecha o izquierda toda la gráfica, en particular, su asíntota vertical. Pero la forma de la gráfica no cambia.
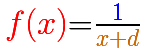
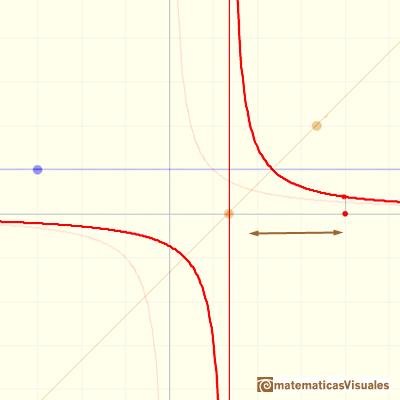
Si cambiamos la pendiente de la recta que representa al denominador el resultado es una contracción o expansión a lo largo del eje de ordenadas. Este efecto de contracción o expansión también se consigue modificando la coordenada y del punto azul (valor del numerador).
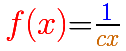
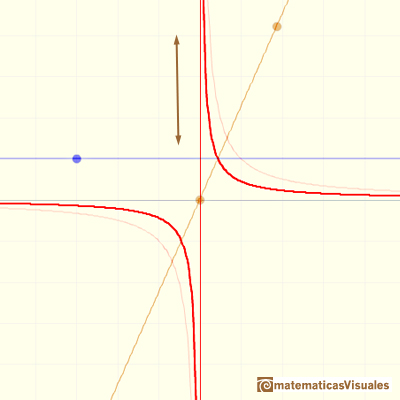
Combinando ambos tenemos una traslación y una contracción (o expansión):
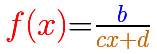
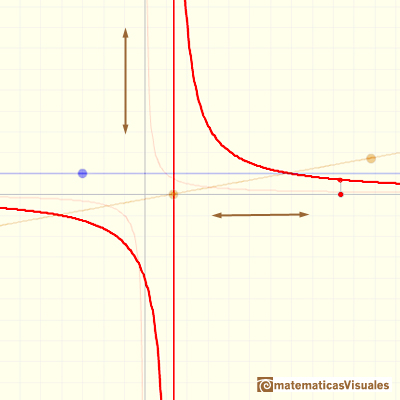
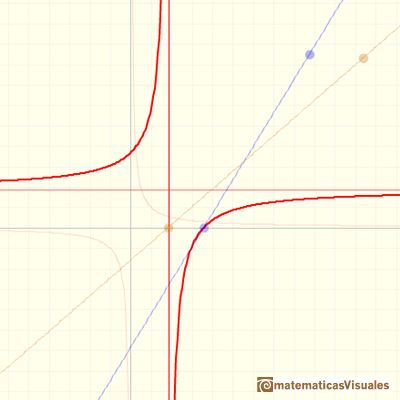
Vamos a considerar ahora el caso más general de función racional lineal en el que tanto el numerador como el denominador son polinomios de grado 1, es decir, dos rectas (con c distinto de 0).
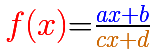
En el siguiente vídeo controlamos funciones racionales lineales modificando dos rectas, una para el numerador y otra para el denominador. En particular podemos explorar qué ocurre cuando ambas rectas se cortan sobre el mismo valor del eje de abcisas. Entonces vemos que la asíntota vértical deja de existir. Estas situaciones también se reproducen en el vídeo del inicio de la página, como veremos más adelante.
El dominio de una función racional lineal es:
Una función racional lineal tiene una asíntota horizontal:
Si el numerador y el denominador no tienen un factor común entonces la función racional tiene una asíntota vertical:
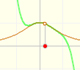
Cuando las dos rectas tienen la misma raíz (el numerador y el denominador tienen un factor común y las dos rectas se cortan sobre el eje de abcisas) tenemos un 'agujero', una 'singularidad evitable'. A veces se dice que es una 'discontinuidad evitable'. La idea es que podemos simplificar la fracción y obtenemos una nueva función que es distinta aunque casi igual que la original pero que tiene un dominio mayor (pues 'rellenamos el agujero').
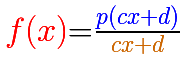
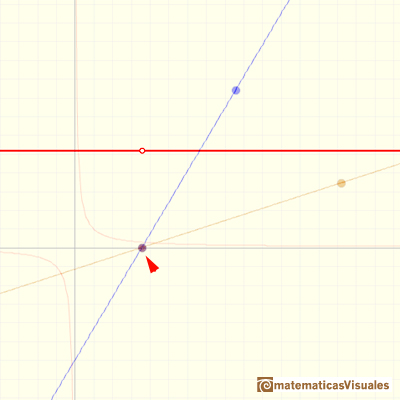
Una singularidad evitable es un valor de x para el que se le puede asignar un valor de modo que la nueva función sea continua en ese punto.
Las funciones racionales pueden tener dos tipos de singularidades: En algunos casos la función tiene una asíntota vertical (la singularidad es esencial o no evitable) y en otros casos tiene un 'agujero' (singularidad evitable).
Es interesante distinguir dos tipos de funciones racionales cuando están expresadas como cociente de polinomios: funciones racionales propias e impropias. Una función racional propia es aquella que tiene el grado del numerador menor que el grado del denominador. En otro caso decimos que es impropia. Por ejemplo, la función 1/x es propia pero, en muchos casos, como hemos visto en los ejemplos anteriores, una función racional lineal puede ser impropia pues tanto el numerador como el denominador tienen grado 1.
Si una función racional es impropia podemos dividir el numerador y el denominador y podemos escribir la función racional como suma de un polinomio y una función racional propia:
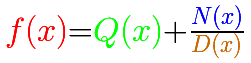
El polinomio controla el comportamiento de la función cuando x se hace grande en valor absoluto. Esto es debido a que una función racional propia contribuye muy poco a los valores de la función para valores grandes de |x|.
En el caso de las funciones racionales lineales, al dividir obtendremos un cociente que es un número:
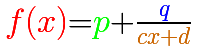
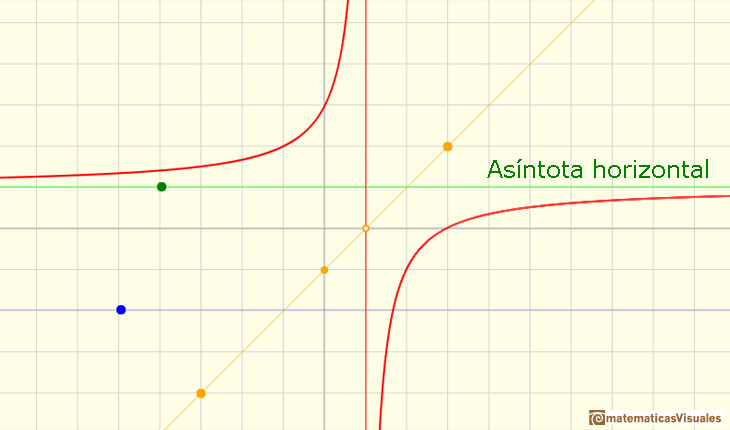
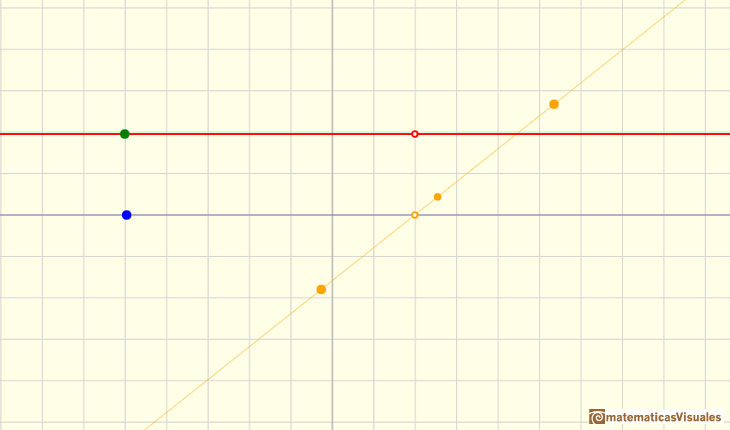
En la aplicación interactiva podemos jugar con estos tres elementos de una función racional lineal: un número (el cociente, p, en verde, determina la asíntota horizontal), otro número en el numerador de la expresión racional propia (q, en azul, es también una recta horizontal) y una recta en denominador (en color naranja)
Podemos comprobar cómo el número p controla el comportamiento 'en el infinito' de la función y cómo afectan el numerador y el denominador a la forma de la gráfica de la función.
Todas las funciones racionales lineales "pueden escribirse de un modo análogo, separando su 'parte entera'. En consecuencia, las gráficas de todas las funciones racionales lineales [no degeneradas] son hipérbolas (trasladadas diferentes distancias a lo largo de los ejes de coordenadas y contraídas o expandidas a lo largo del eje de ordenadas)". ["Functions and Graphs", pág. 64]
En este caso, la asíntota horizontal es:
Por ejemplo:
Podemos escribir el caso degenerado (con un agujero):
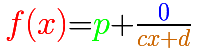
INVESTIGA
Modifica los valores que definen la función racional real en la aplicación interactiva y estudia cómo cambia la posición de las asíntotas y la forma de la gráfica.
Reproduce la situación en la que tenemos una discontinuidad evitable.
La descomposición de la función racional lineal como un número y una fracción racional propia nos ayuda a ver si cada una de las ramas de la hipérbola 'va por arriba' o 'por abajo' de la asíntota horizontal cuando consideramos valores 'grandes' en valor absoluto de la x. ¿Cómo podemos razonar? Se puede tener en cuenta que la parte racional propia es 'muy pequeña' cuando x es 'muy grande' pero unas veces es positiva y otras negativa. Busca ejemplos.
Así se puede generar una singularidad evitable:
Para ver este tipo de vídeos puedes seguir este enlace:
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES