En esta página se pretende revisar el concepto de continuidad desde un punto de vista básico e intuitivo.
Para profundizar en este concepto de continuidad de funciones se recomienda el texto clásico 'Calculus' de Michael Spivak.
Aquí nos aproximaremos a este concepto de continuidad de funciones desde un punto de vista más básico.
Lo primero que tenemos que tener en cuenta cuando hablamos de continuidad es que la frase
'Una función es continua cuando la puedo dibujar sin levantar el lápiz del papel' es muy imprecisa.
Puede ser confusa por dos motivos. El primero es porque nos habla de la propiedad de continuidad como algo referido a toda la función, es decir, la función vista en su conjunto. Veremos que para definir la continuidad empezamos definiendo el concepto para un valor x=a. Decimos que es una propiedad LOCAL. De ahí extendemos la definición a un intervalo.
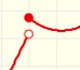
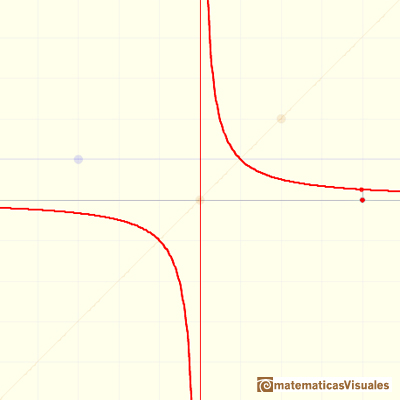
Veremos que una función racional como f(x)=1/x no la puedo dibujar sin levantar el lápiz del papel y, sin embargo, podemos decir correctamente que esa función es continua en todo su dominio.
Un segundo motivo es que el dibujo de una gráfica puede esconder discontinuidades que no pueden verse aún utilizando el más potente de los microscopios. Veremos ejemplos de esto cuando hablemos de las discontinuidades evitables, por ejemplo.
El asunto de la continuidad se define como 'continuidad en un punto' o 'continuidad para x=a'.
Es decir, que es un CONCEPTO LOCAL, que trata del comportamiento de una función 'alrededor' del valor x=a. No importando el comportamiento de la función para valores 'no tan cercanos' a x=a. Esto es fundamental. Concretar esta idea, hacerla precisa, será trabajo del siguiente curso, ya en la Universidad.
Posteriormente, una vez que hayamos podido comprobar que la función es continua en todos (y cada uno) de los números de un intervalo, podremos decir que la función es continua en ese intervalo o en todos los números reales, si es el caso.
Un concepto de los más básico cuando estudiamos una función es el de 'dominio de definición' de la función.
Es lo primero que tenemos que tener claro cuando estudiemos la continuidad de una función.
El dominio de una función de las que estudiamos aquí es un subconjunto de los números reales, que puede ser el conjunto de todos los números reales.
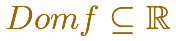
Si no se dice lo contrario, el dominio de definición de una función es el subconjunto de los números reales más grande que la función admita.
Por ejemplo, cualquier función polinómica tiene como dominio todos los números reales, si no se dice lo contrario.
Es muy habitual acotar, acortar, ese dominio de definición 'natural' de una función. Un ejemplo muy sencillo, la variable independiente es el lado de un cuadrado y la variable dependiente es la diagonal de ese cuadrado. En este caso, los números negativos no pueden ser del dominio pues estaríamos considerando longitudes de lados negativas. Y, de momento, no las consideramos.
Por lo tanto, en este ejemplo, el dominio de esa función sería:
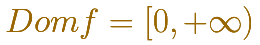
Incluso en este caso tenemos dudas pues si consieramos como valor aceptable el 0 estamos hablando de un cuadrado de lado 0. Sería un caso que decimos 'degenerado': el cuadrado ha dejado de tener dimensión.
En lo que sigue a continuación, vamos a hacer importantes simplificaciones sobre las funciones que vamos a considerar.
La primera es que, salvo algunos casos sencillos, el dominio va a ser siempre el dominio 'natural', el más grande que adminte una función.
En resumen, cuando nos pregunten cualquier cosa sobre una función, lo primero que tenemos que tener claro es el dominio de esa función.
Si a pertenece al dominio de f
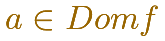
esto querrá decir que puedo calcular f(a), que existe f(a) y que es un número real.
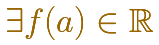
Esto va a ser fácil para nosotros, pues las funciones que vamos a considerar vienen dadas por fórmulas (relativamente) sencillas.
Si no existe f(a), estrictamente hablando, nada podemos decir de la 'función en x=a' pues no existe. Desde luego, la función no podrá ser continua en x=a pues ni tan siquiera existe.
Más adelante veremos qué podemos decir en relación con el infinito.
A veces empleamos esta expresión 'en un punto x=a' y alguien puede decir que 'x=a' no es ningún punto. Y tiene toda la razón.
La expresión se refiere, e insiste en ello, que debe existir el punto en la gráfica de la función
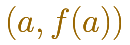
En ese sentido usaremos esa expresión 'en un punto x=a';
Ya hemos comentado que, en algunas ocasiones, emplearemos la expresión un tanto incorrecta 'en un punto x=a'.
Pero x=a tiene dos sentidos claros y distintos:
El primero es 'el valor de la variable independiente x es a'.
El segundo se refiere a la recta vertical que pasa por x=a y que contiene los infinitos puntos
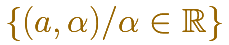
Notar que esa es la expresión algebraica de una recta en 'implícitas' pero no es una función, en el sentido que nosotros usamos.
Uno de los usos de esta expresión es cuando hablamos de asíntota vertical.
Por ejemplo, esta función tiene una asíntota vertical x=0:
La definición de CONTINUIDAD de una función en x=a se suele hacer usando límites.
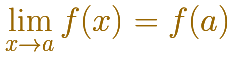
Hay que tener claro que esta definición es muy compacta y se puede descomponer en tres 'pruebas' o 'tests' que tiene que pasar nuestra función en x=a para poderse afirmar que es continua en x=a.
Esas tres 'pruebas' se enumeran a continuación.
TEST 1
Es muy fácil pues se trata de probar que
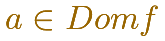
O lo que es lo mismo
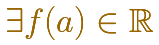
Resulta sencillo en general. Si resulta que no puedo calcular ese valor ya puedo concluir que la función no es continua en x=a.
TEST 2
Esta es la prueba que puede ser un poco más dificil para nosotros pues se enuncia usando límites
Para pasar esta segunda prueba debe existir el límite, es decir, que ese límite es un número real.
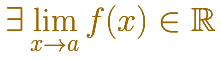
Comprobar esto puede ser sencillo y veremos casos en los que lo haremos directamente
En algunos casos tendremos que calcular por separado los límites laterales.
Por la derecha debe ser un número real:
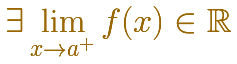
Por la izquierda debe ser un número real:
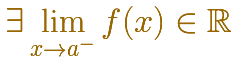
Si resulta que son iguales
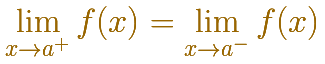
entonces el límite existe (y esto quiere decir que es un número real)
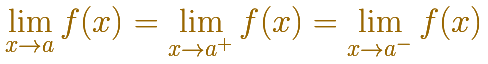
Si alguno de estos límites no existe o existen pero son distintos ya podemos concluir que la función no es continua en x=a.
TEST 3
Si hemos pasado el Test 1 y el Test 2, es decir, que tenemos dos números reales, entonces para comprobar la continuidad solo falta comprobar que ambos números son iguales.
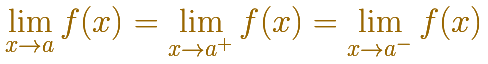
Si resultara que esos dos números reales son distintos, puedo concluir que la función no es continua en x=a.
En resumen, la función tiene que pasar tres pruebas pero la única que puede ser un poco complicada es el Test 2.
Tengamos en cuenta que somos nosotros los que tenemos que comprobar que la función pasa esas tres pruebas.
Si solo nos preguntan la continuidad basta con que falle alguno de los test para concluir que no es continua en x=a y no tenemos que seguir pasando más test.
Sin embargo, si nos piden especificar algo en relación con qué tipo de discontinuidad tenemos entonces tendremos que seguir trabajando. Eso ya lo veremos. Según falle la comprobación en un test u otro, esto nos ayudará a determinar qué tipo de discontinuidad tenemos.
Un resultado muy importante es el siguiente:
Las funciones polinomicas, racionales, exponenciales, logarítmicas y trigonométricas son continuas en todo su dominio.
También la composición de varias funciones de estos tipos.
Todos estos resultados hay que probarlos y eso lo haréis el próximo curso en la Universidad.
Pero para nosotros va a ser una herramienta muy potente. Nos va a permitir usar un 'truco' para calcular límites.
Cuando te expliquen con un poco de rigor (o con mucho rigor) el concepto de límite verás que se insiste en que se estudia el comporamiento de una función para valores próximos a x=a pero distintos.
Sin embargo, podemos usar nuestro 'truco' y, a la hora de calcular un límite, lo primero que hacemos es justamente sustituir la variable por el valor hacia el que tiende la x. Si esa cuenta se puede hacer sin problemas ese va a ser el valor del límite.
Este primer intento de cálculo de un límite puede fallar por varios motivos, por ejemplo: intento dividir entre 0, intento calcular una raíz cuadrada de un número negativo (el resultado no sería real) o intento calcular el logaritmo de un número menor o igual que 0.
En esos casos me las tendré que ingeniar para calcular el límite con otros procedimientos o para poder afirmar que el límite no existe.
En el siguiente enlace empezamos a estudiar la continuidad de familias de funciones definidas a trozos dependientes de un parámetro.
ANTERIOR
MÁS ENLACES
