Suma de una serie geométrica
Nos planteamos la suma de una serie geométrica.
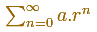
Cuando la razón es mayor que 1 el término general crece por encima de cualquier cota y la suma no puede converger.
Cuando la razón es menor que 1 la serie es convergente y su suma es:
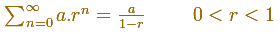
Queremos mostrar un caso particular, cuando la razón es
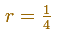
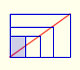
Entonces, la serie que queremos sumar se puede representar así:
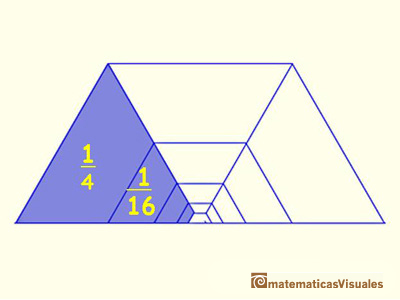
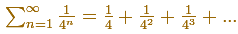
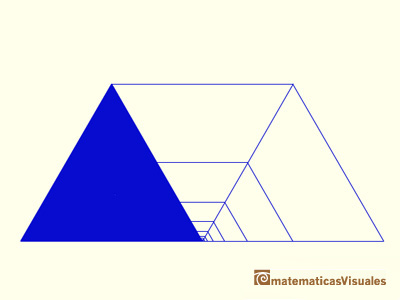
Y la suma de la serie geométrica cuya razón es un cuarto es:
SIGUIENTE
La serie geométrica de razón 1/2 es convergente. Esta serie se puede representar usando un rectángulo y dividiéndolo por la mitad sucesivamente. Aquí usamos una proporción de modo que todos los rectángulos son semejantes.
ANTERIOR
Representación gráfica de progresiones geométricas. Suma de los términos de una sucesión geométrica. Series geométricas.
MÁS ENLACES
Estudiamos varias propiedades de las funciones exponenciales, sus derivadas y una introducción al número e.
A partir de una función positiva decreciente podemos definir series y aplicar el test de la integral. El test de la integral es un criterio que nos puede ayudar a decidir si una serie converge o diverge. Además, si la serie converge nos dará cotas.
La integral de las funciones potencia era conocida por Cavalieri para n=1 hasta n=9. Fermat, entre otros, fue capaz de resolver este problema. Su técnica es un buen ejemplo del uso de progresiones geométricas.
El papel que solemos utilizar tiene un tamaño estándar. Estos rectángulos de papel, que llamamos DIN A, son semejantes y cada tamaño se obtiene del anterior partiéndolo por la mitad.
Una rotación dilatativa se obtiene combinando una rotación y una dilatación con el mismo centro.
En una espiral equiangular el ángulo entre el radio vector y la tangente es constante.
Geométricamente, la multiplicación por un complejo es una transformación del plano que consiste en una rotación y una expansión o contracción (rotación dilatativa).
Una progresión geométrica compleja está relacionada con las espirales equiangulares.