Las distribuciones t de Student fueron descubiertas por William S. Gosset (1876-1937) en 1908 cuando trabajaba para la compañía de cervezas Guinness en Dublín (Irlanda). No pudo publicar sus descubrimientos usando su propio nombre porque Guinness había prohibido a sus empleados que publicaran información confidencial. Gosset firmó sus publicaciones usando el nombre de "Student". Gosset tenía buena relación con Karl Pearson que había sido su maestro. Necesitaba una distribución que pudiera usar cuando el tamaño de la muestra fuera pequeño y la varianza desconocida y tenía que ser estimada a partir de los datos. Las distribuciones t se usan para tener en cuenta la incertidumbre añadida que resulta por esta estimación. Fisher comprendió la importancia de los trabajos de Gosset para muestras pequeñas.
Si el tamaño de la muestra es n entonces decimos que la distribución t tiene n-1 grados de libertad. Hay una distribución t diferente para cada tamaño de la muestra. Estas distribuciones son una familia de distribuciones de probabilidad continuas. Las curvas de densidad son simétricas y con forma de campana como la distribución normal estándar. Sus medias son 0 y sus varianzas son mayores que 1 (tienen colas más pesadas). Las colas de las distribuciones t disminuyen más lentamente que las colas de la distribución normal. Si los grados de libertad son mayores más próxima a 1 es la varianza y la función de densidad es más parecida a la densidad normal.
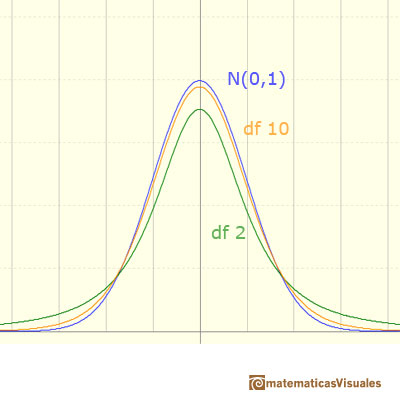
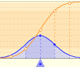
Cuando n es mayor que 30, la diferencia entre la normal y la distribución t de Student no suele ser muy importante. En la imagen podemos ver varios ejemplos de funciones de distribución acumulada.
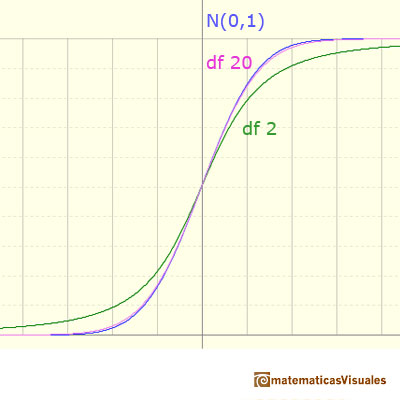
En Probabilidades en Distribuciones t-Student puedes ver una comparación más precisa entre las distribuciones t-Student y la normal estándar.
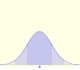
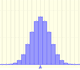
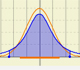
En el applet podemos ver varios ejemplos de distribución t de Student junto con la normal estándar.
Se aprecia cómo cuando el parámetro es 25 la distribución es muy parecida a la normal estándar.
Los puntos grises controlan la escala vertical y horizontal de la gráfica y pulsando el boton derecho y arrastrando podemos moverla a derecha e izquierda.
ENLACES