Cuando se modela una situación en la que hay n ensayos independientes con una probabilidad p de "éxito" constante en cada ensayo utilizamos una distribución binomial.
Por ejemplo, el lanzamiento de n monedas iguales y contamos como éxito el sacar cara. La probabilidad de sacar cara puede ser cualquier valor entre 0 y 1.
Una distribución binomial se caracteriza por dos parámetros: n (un número natural) y p un número entre 0 y 1.
Si una variable aleatoria X sigue una distribudión binomial con parámetros n y p podemos escribir:
La probabilidad de obtener exáctamente k éxitos en n experimentos viene dada por la función de densidad (o función de masa):
donde
Esta expresión es el coeficiente binomial, "n sobre k", o el número de modos posibles de obtener k éxitos en n observaciones. Los coeficientes binomiales forman las filas del triángulo de Pascal y se puede calcular usando factoriales:
Cuando p = 0.5 la función de densidad es simétrica:
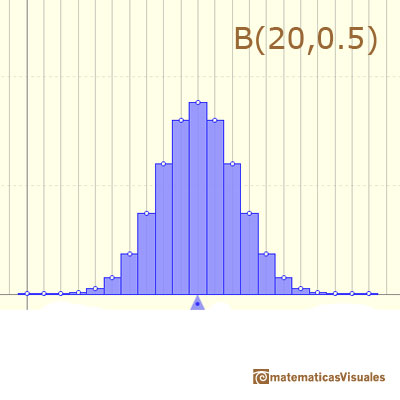
En otro caso la función de densidad es asimétrica:
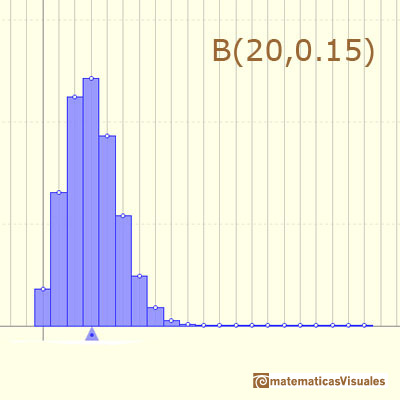
La media y la varianza de la distribución binomial son:
El applet está desarrollado en HTML5 y puede ser manejado con ratón o con pantalla táctil desde una tableta o teléfono móvil.
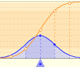
Podemos cambiar el parámetro n de la distribución binomial. La media está representada por un triángulo azul que podemos ver como el punto de equilibrio. Arrastrando este triángulo modificamos la media y, por tanto, el parámetro p.
Los puntos rojos son controles verticales y horizontales de la escala.
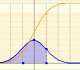
Podemos mostrar la curva normal que tiene la misma media y varianza que la distribución binomial.
En algunos casos, esta curva normal es una buena aproximación de la binomial y puede usarse para hacer cálculos.
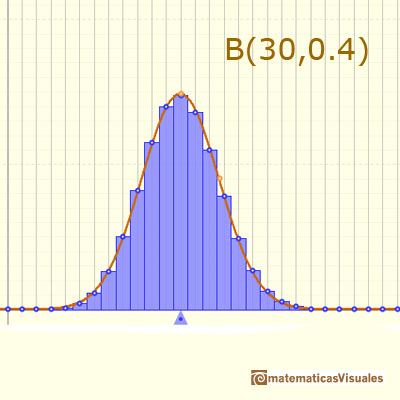
Podemos ver por qué se recomienda en estos casos extender el intervalo para calcular la probabilidd de la binomial en 0.5 por arriba y por debajo cuando usamos la distribución normal para aproximar la probabilidad (ajuste de corrección de continuidad).
Por ejemplo:
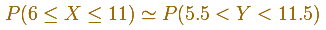
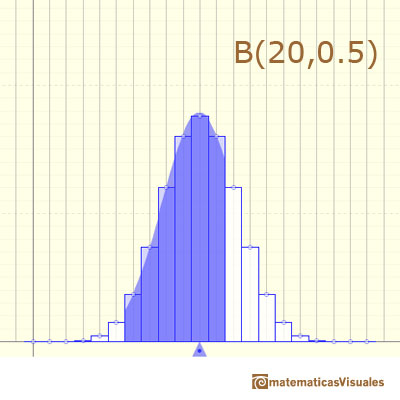
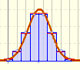
En otros casos, esta curva normal no es una buena aproximación a la distribución binomial:
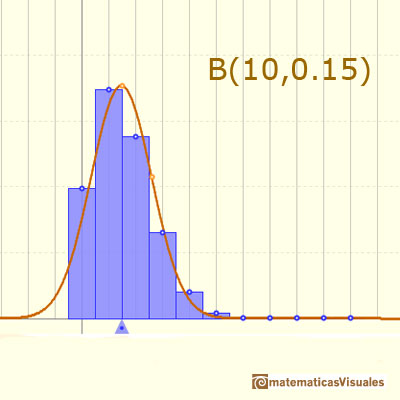
Incluso con la corrección de continuidad la aproximación no es buena:
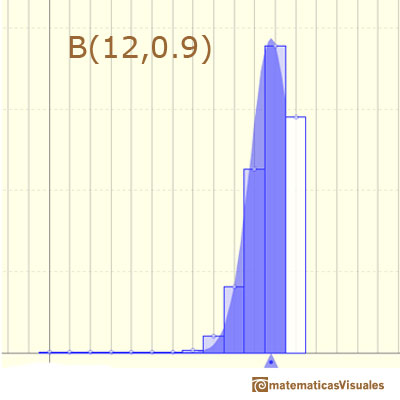
Podemos ver esta aproximación normal a la distribución binomial con más detalle para comprender mejor en qué casos se puede utilizar con una precisión razonablemente buena.
 SIGUIENTE
SIGUIENTE
MÁS ENLACES