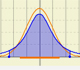
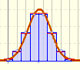
Las distribuciones normales son una familia de distribuciones que dependen de dos parámetros: la media y la varianza. La raíz cuadrada positiva de la varianza se llama desviación típica o estándar.
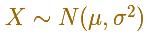
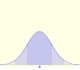
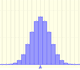
El caso más sencillo es cuando la media es 0 y la desviación típica 1. Se llama la distribución normal estándar.
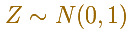
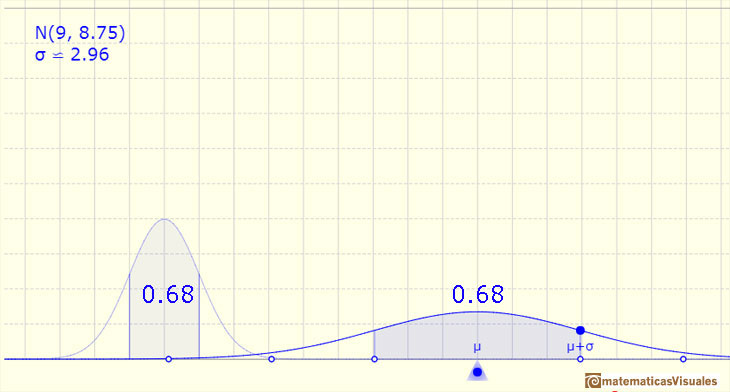
Una importante propiedad de las distribuciones normales es que si consideramos intervalos centrados en la media y con una amplitud determinada proporcional a la desviación típica, la probabilidad de esos intervalos es constante independientemente de la media y la desviación típica de la distribución normal considerada.
Por ejemplo, si consideramos un intervalo centrado en la media y de amplitud una desviación típica hacia arriba y hacia abajo la probabilidad siempre es la misma y su valor es 0.68 aproximadamente.
Este valor es el área bajo la función de densidad (la campana, también llamada campana de Gauss) entre esos dos valores de la variable:
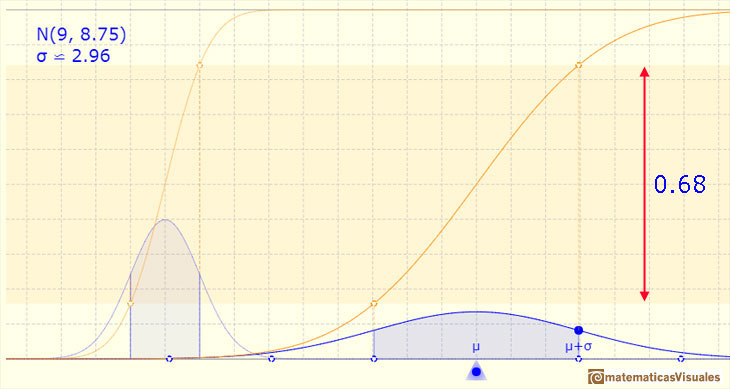
Si consideramos el caso de la distribución normal estándar podemos escribir:
En el caso general de una distribución normal:
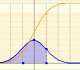
El método que podemos usar para calcular él área es usar la función de distribución (acumulada). Entonces el área, es decir, la probabilidad se calcula como la resta de dos valores:
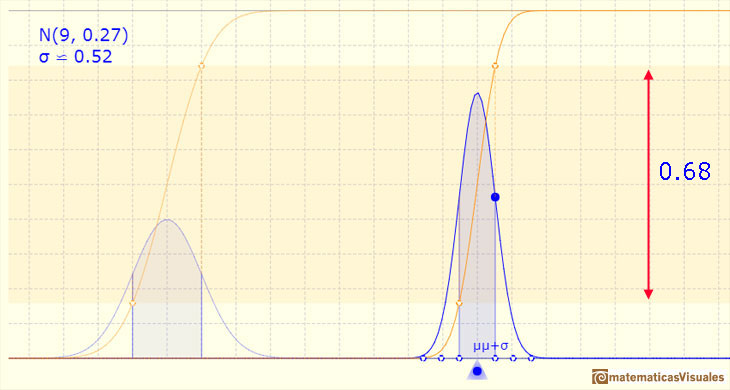
Podemos ver que este valor no cambia si modificamos la media y la desviación típica de la distribución normal:
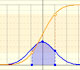
Si la amplitud del intervalo es de dos desviaciones típicas arriba y abajo, entonces la probabilidad es 0.95 aproximadamente.
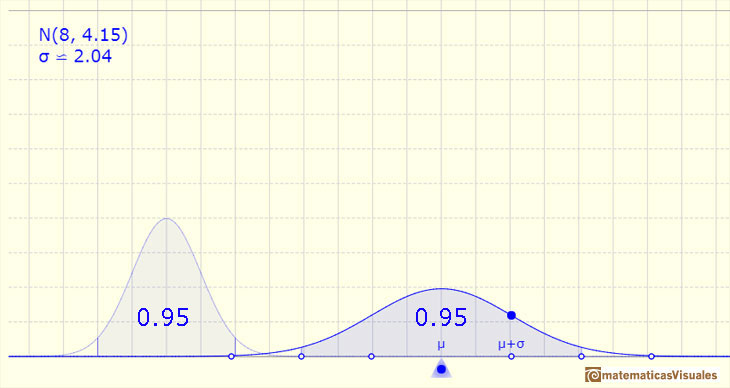
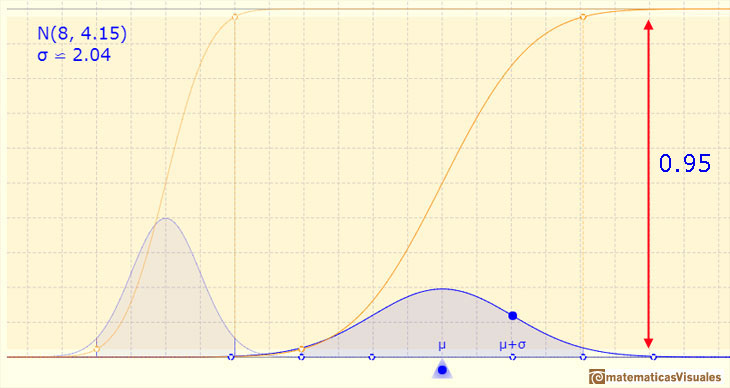
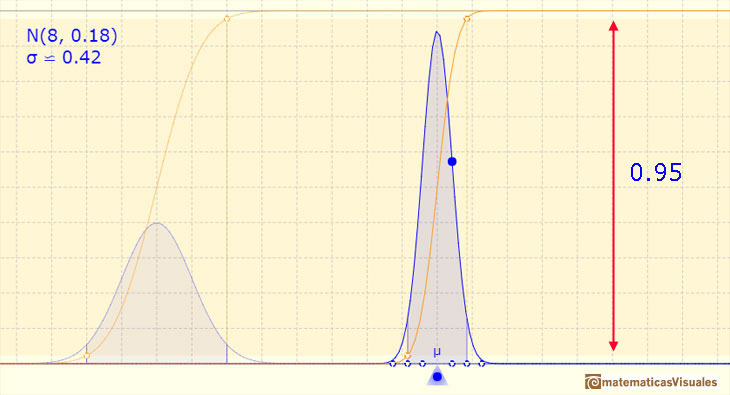
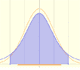
Si la amplitud del intervalo es de tres desviaciones típicas arriba y abajo, entonces la probabilidad es 0.997 aproximadamente.
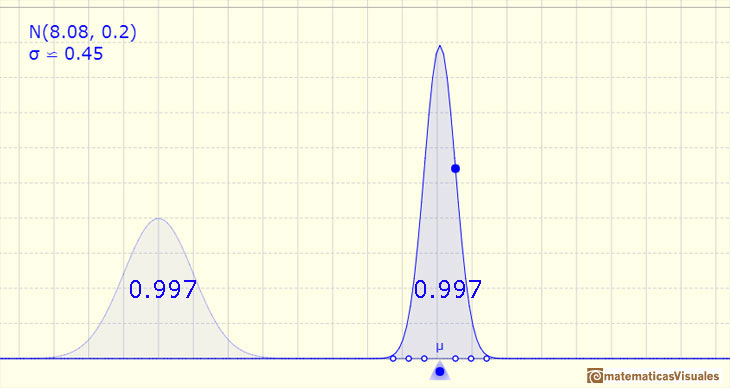
La probabilidad es casi 1 pero, ampliando la imagen, podemos ver que todavían quedan unas 'colas' por cubrir.
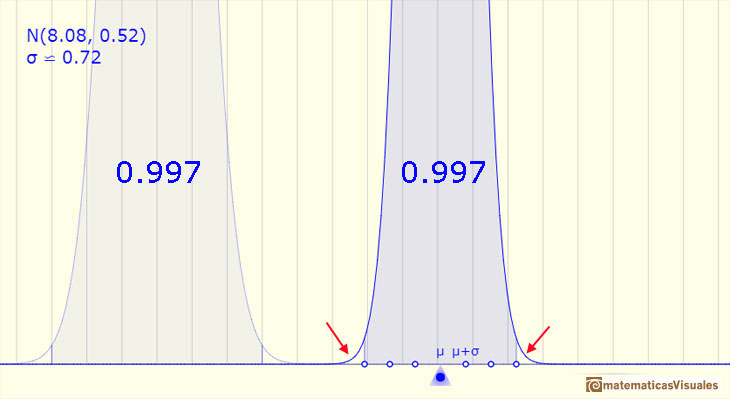
Estos valores de probabilidad (0.68, 0.95 y 0.997) para intervalos de una, dos y tres desviaciones típicas en torno a la media de una variable normalmente distribuida se usan a menudo en los cálculos estadísticos.
Podemos modificar los parámetros de la distribución normal.
La media está representada por un triángulo y se puede interpretar como un punto de equilibrio. Al arrastrarlo se modifica la media.
Arrastrando el otro punto sobre la curva (que es uno de los dos puntos de inflexión de la curva) se modifica la desviación típica.
Podemos ver la función de distribución (acumulada) y cómo cambia cuando modificamos la media (una simple traslacion) y la desviación típica (reflejando una mayor o menor dispersión de la variable).
Los puntos rojos controlan la escala vertical y horizontal de la gráfica.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
 ANTERIOR
ANTERIOR
MÁS ENLACES