


Este artículo es una traducción de "Kepler: The Volume of a Wine Barrel" que fue publicado en Convergence en 2012 ("Convergence: Where Mathematics, History, and Teaching Interact"), la revista digital de la Mathematical Association of America.
Con el paso del tiempo, la versión original presenta algunos problemas con las aplicaciones interactivas. Puede consultarse la versión inglesa correcta en matematicasVisuales
El principal objetivo de este artículo es mostrar algunas contribuciones de Kepler en el desarrollo del Cálculo de un modo visual e interactivo.
Durante la centuria anterior a Newton y Leibniz los trabajos de los matemáticos griegos fueron populares, especialmente los trabajos de Arquímedes. Se desarrollaron técnicas infinitesimales para calcular áreas y volúmenes, y Johannes Kepler (1571-1630) contribuyó a estos desarrollos.
Su interés en el cálculo de áreas y volúmenes se intensificó a partir de un incidente que ocurrió cuando se casó por segunda vez en Linz, Austria. Kepler había comprado un barril de vino para la boda y el método que usó el comerciante de vinos para medir el volumen del tonel le llamó la atención.
Esto inspiró a Kepler para estudiar cómo calcular áreas y volúmenes y escribió un libro sobre este tema titulado 'Nova stereometria doliorum vinariorum' (que podemos traducir por 'Nueva geometría sólida de los barriles de vino'), en 1615, que fue su mayor contribución al desarrollo del cálculo integral.
Este asunto del barril de vino también llevó a Kepler a considerar otro problema de cálculo diferencial, un problema de máximos, de optimización: ¿Cuál es el mejor diseño para un barril de modo que se maximize su volumen?. Actualmente podríamos resolver este tipo de problemas usando derivadas pues sabemos que en un valor máximo (o mínimo) de una función difererencible la derivada de la función es cero.
Fermat fue el primero en relacionar problemas de máximos y mínimos con tangentes de curvas: en un máximo o en un mínimo la pendiente de la tangente a la gráfica de la función es cero. Kepler fue capaz de mostrar que, a pesar de pequeñas diferencias, las proporciones de los barriles que los mercaderes usaban en Austria eran aquellos para los que el procedimiento que usaban para calcular su volumen era bastante preciso.
Johannes Kepler (1571 - 1630) fue un matemático, astrónomo y astrólogo alemán. Fue una figura clave para la revolución científica del siglo XVII.
Vivió después de Copernico y fue partidario del modelo heliocéntrico del universo.
Kepler trabajó con Tycho Brahe y usó los datos de las precisas observaciones de Brahe para formular su descubrimiento más famoso que conocemos como las tres leyes de Kepler del movimiento planetario. Posteriormente, Newton probó que las leyes de Kepler pueden deducirse a partir de las leyes del movimiento y la gravitación universal de Newton.
Como matemático, Kepler hizo descubrimientos en el campo de los poliedros, trabajó en el problema de empaquetamiento de esferas iguales, estuvo interesado en los logaritmos y estudió volúmenes de sólidos de revolución.
El objetivo principal de esta página es mostrar algunas contribuciones de Kepler al desarrollo del Cálculo.
Kepler vivió antes que Newton y Leibniz. Durante el siglo XVI y principios del XVII las obras maestras de los matemáticos griegos como 'Los elementos' de Euclides, las 'cónicas' de Apolonio o los trabajos de Arquímedes se estudiaron seriamente.
Muchos matemáticos refinaron el método de exhaución y lo aplicaron a una amplia variedad de nuevos problemas de cuadraturas (áreas) y cubaturas (volúmenes). Otro punto de interés fue la determinación de centros de gravedad de sólidos (ver el libro de Margaret Baron, página 90, sobre la importancia de los centros de gravedad en el desarrollo del Cálculo).
Los matemáticos del Renacimiento estaban más interesados en nuevos resultados y métodos de descubrimiento que en demostraciones rigurosas. Usaron libremente conceptos intuitivos sobre el infinito para obtener métodos infinitesimales para solucionar problemas de áreas y volúmenes.
Kepler y Cavalieri fueron dos matemáticos clave en la invención de estos métodos infinitesimales.
La primera mujer de Kepler murió y Kepler quedó viudo con varios hijos. En 1613 se volvió a casar celerando su boda en Linz, ciudad austriaca. Kepler compró un barril de vino para la boda pero no le convenció el método que usó el comerciante para medir el volumen del barril y determinar el precio.
Como consecuencia de este incidente, Kepler estudió varios problemas sobre volúmenes, entre ellos, cómo calcular correctamente el volumen de un barril de vino y cómo encontrar proporciones que optimizaran ese volumen.
Publicó un libro en 1615 titulado "Nova Stereometria doliorum vinariorum" ("Nueva estereometría o cálculo de volúmenes de barriles de vino"). Podemos consultar una versión original en The Posner Library)
El dibujo de la derecha muestra un barril tumbado y muestra cómo el comerciante de vinos determinaba el volumen del barril y, por lo tanto, el precio del vino. El mercader introducía una vara por el agujero del barril (en el dibujo, en el centro de la parte superior) hasta un extremo opuesto de una tapa del barril (abajo a la derecha o a la izquierda). La longitud de la vara insertada en el barril determinaba el precio que el comerciante pedía.
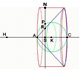
Kepler tuvo una idea fundamental para calcular con precisión volúmenes de cuerpos sólidos, en particular, barriles. Para Kepler un sólido estaría formado por numerosas capas finas cilíndricas y trató el volumen como la suma de todos esos cilindros. (Klein, p. 209)
La siguiente aplicación interactiva muestra cómo Kepler podía refinar su aproximación usando más y más cilindros. En el caso de los barriles y otros cuerpos de revolución, estas capas se tomaban perpendiculares al eje del barril. Cada diámetro sería igual al del barril a la altura correspondiente. El grosor de cada cilindro puede ser tan fino como uno quiera imaginar. Es decir, las capas cilíndricas están apiladas y todas juntas forman el barril.
Según Otto Toeplitz (p.83):"Considerando estas aproximaciones cada vez más finas de barriles de diferentes formas, consultó los trabajos de Arquímedes y descubrió que su método de indivisibles le había permitido obtener resultados de un modo mucho más simple y más general que Arquímedes, quién había estado luchando con demostraciones difíciles y engorrosas.
Lo que Kepler no podía sospechar era que Arquímedes había encontrado sus resultados usando el mismo método de indivisibles (¡pues 'El Método' estuvo perdido hasta 1906!)".
'El Método' es un trabajo de Arquímedes donde describe cómo encontró muchos de sus resultados sobre áreas y volúmenes. Su enfoque aquí también lo podemos considerar intuitivo. Después Arquímedes publicaba demostraciones precisas de sus descubrimientos.
Cuando un viejo manuscrito de este libro fue encontrado fue estudiado por Heiberg. Actualmente, y después de varias peripecias, este libro esta depositado en The Walters Art Museum en Baltimore. Podemos aprender mucho de este fascinante libro y de su historia en Archimedes: The Palimpsest Project (Noviembre 2018: este sitio web tiene muchos enlaces rotos. Es una pena aunque todavía se puede encontrar información).
|
Archimedes' Method for Computing Areas and Volumes
Artículo de Gabriela Sanchis en Loci Convergence donde explica el método de Arquímedes basado en la Ley de la palanca. |
|
Arquímedes en matematicasVisuales - Área de un segmento parabólico
Arquímedes usó métodos infinitesimales para descubrir áreas y volúmenes mil ochocientos años antes que Kepler o Cavalieri. |
Kepler expuso sus resultados sobre los barriles y otros sólidos en su libro de 1615 "Nova Stereometria doliorum vinariorum" ("Nueva estereometría o cálculo de volúmenes de barriles de vino").
La palabra Stereometria proviene del griego antiguo stereos que significa sólido o tridimensional y de metron que significa medir o medida. Entonces Stereometria significa el arte de medir volúmenes o sólidos. A partir del título de libro podríamos usar Doliometría que proviene del latín dolium que significa jarra grande de alfarería y, posteriormente, barril.
Este libro es un trabajo sistemático sobre el cálculo de áreas y volúmenes usando técnicas infinitesimales. Se basa en los trabajos de Arquímedes y se centra en sólidos de revolución e incluye cálculos exactos o aproximados de volúmenes de unos noventa de esos sólidos. (Edwards, p. 102). Actualmente usamos el cálculo integral para resolver ese tipo de problemas.

|
Versión original en Latín en The Posner Memorial Collection
Versión original en Latín en The Posner Memorial Collection,Carnegie Mellon University Libraries, Pittsburgh PA Versión original en alemán en ConvergenceDos páginas de la versión original en alemán de "Nova Stereometria". |
Según C.H. Edwards (p. 102), "La técnica que usó Kepler [en su Estereometría consistió en] diseccionar un sólido dado en una... infinidad de piezas infinitesimales, o sólidos 'indivisibles', de un tamaño y forma conveniente para la solución del problema particular".
Entonces Kepler sumaba los volúmenes de esas piezas componentes para obtener el volumen de un solido dado. Los elementos infinitesimales de Kepler tenían que tener la misma dimensión que el cuerpo que quería medir. Es decir, si quería calcular un área entonces sumaba elementos de área y si quería calcular un volumen consideraba elementos infinitesimales sólidos con volumen.
Kepler comienza su trabajo con el problema de determinar el área de un círculo. Considera el círculo como un polígono regular con un infinito número de lados y, por lo tanto, compuesto por una infinidad de triángulos infinitesimales cuyas bases son los lados del polígono y sus alturas se pueden considerar el radio del círculo, coincidiendo los vértices opuestos a las bases en el centro del círculo. Como el área de un triángulo es la mitad del producto de su base por su altura el área total del círculo viene dada por la mitad del producto del perímetro de la circunferencia y el radio.

|
Kepler en matematicasVisuales - El área de un círculo
Kepler usó un procedimiento infinitesimal intuitivo para calcular el área de un círculo. |
De un modo análogo, considerando una esfera como compuesta por un número infinito de conos infinitesimales cuyos vértices están en el centro de la esfera y cuyas bases forman la superficie de la esfera, Kepler nos muestra que el volumen de una esfera es un tercio del producto de la superficie esférica y el radio. (Recordamos que el volumen de un cono es un tercio del producto del área de su base por su altura).
Kepler también rotó un círculo en torno a la recta externa al círculo y calculó, usando métodos infinitesimales, el volumen del toro (la figura en forma de rosquilla) que se genera. Extendió su trabajo a otros sólidos que no habían sido estudiados por los antiguos. Algunos de sus cálculos son anticipaciones destacables de resultados que se obtuvieron posteriormente usando cálculo integral.

|
Kepler en Mathworld: Limón
Kepler en Mathworld: Manzana En Mathworld podemos ver diferentes sólidos de revolución definidos por Kepler. |
El método que el comerciante de vinos usó para medir el volumen del barril y que tanto extrañó a Kepler consistió en insertar una vara desde del agujero central (S en el diagrama) hasta el lado opuesto de la tapa del barril (en D).
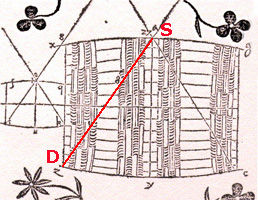
"Entonces él leía la longitud SD=d y determinaba el precio. Esto enfadó a Kepler pues vio que un barril estrecho y más alto tendría el mismo valor SD que uno más ancho y esto indicaría el mismo precio del vino, sin embargo el volumen sería mucho más pequeño". (Toeplitz, pp. 82-83).
Como consecuencia, Kepler trató de determinar las mejores proporciones de un barril de vino de cara a maximizar su volumen. Esto le llevó a considerar varios problemas de optimización que demostraron sen contribuciones muy interesantes al desarrollo del cálculo diferencial. Por ejemplo, Kepler probó que el cubo es el mayor paralelepípedo que puede inscribirse en una esfera (Baron, 115).
Este tipo de problemas de obtener máximos o mínimos no eran nuevos. Por ejemplo, Euclides había demostrado que entre los rectángulos de igual perímetro el cuadrado era el que tenía el área mayor (Toeplitz, p. 80). Pappus de Alejandría, alrededor del año 300 a.C. había probado que de todas las figuras planas equiláteras y equiangulares con el mismo perímetro, la figura con el mayor número de ángulos era la que tenía el área mayor y la figura que tiene la mayor área con un perímetro dado es la del círculo.

|
The Sagacity of Circles: A History of the Isoperimetric Problem
Artículo de Jennifer Wiegert en Convergence. Resumen de la historia del problema de encontrar la región de mayor área con un perímetro dado. |

|
Thinking Outside the Box -- or Maybe Just About the Box
Artículo de David Meel y Thomas Hern en Convergence. Estudian el típico problema de la caja pero de un modo más complejo y realístico y nos muestran cómo puede ser usado para investigar optimización. |
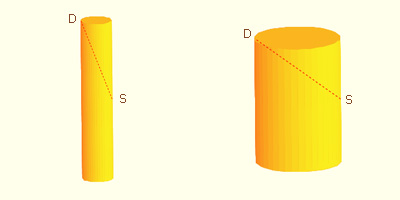
Para optimizar el volumen de un barril, Kepler simplifica el problema. Aproxima el barril por un cilindro que tiene la diagonal d como antes, r sería el radio de la base y h la altura. Con una notación moderna, el volumen V del cilindro es:
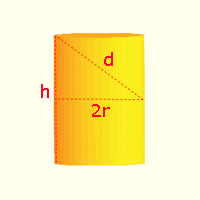
Entonces la relación entre d, h y r puede escribirse, usando el teorema de Pitágoras:
Ahora despejamos r al cuadrado:
Podemos deducir la fórmula del volumen en función de h y d:
Fijando d, la siguiente aplicación interactiva muestra cómo el volumen V cambia cuando modificamos la altura h del barril:
A continuación, Kepler se preguntó: "Si d está fijo, ¿qué valor de h nos da el mayor volumen V?". (Toeplitz, p. 83). Después de algunos cálculos obtiene la respuesta que es:
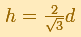
"Esto define un barril de unas determinadas proporciones. Kepler se dio cuenta de que en su tierra natal renana los barriles eran más estrechos y más altos que en Austria, donde su forma era particularmente cercana a la que tenía el máximo volumen para un valor fijo d. Tan cercana que Kepler no podía creer que fuera accidental. Imaginó que siglos atrás alguien había hecho cálculos sobre formas de barriles como él estaba haciendo y que había enseñado a los austriacos a construir barriles de esa manera en particular, especialmente práctica. Kepler mostró que si un barril no satisfacía la especificación matemática
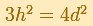
pero se desviaba algo de ella, esto habría tenido solo un pequeño efecto en el volumen, porque cerca de sus máximos una función cambia lentamente"(Toeplitz, p. 83), tal como se ilustra en el siguiente gráfico:
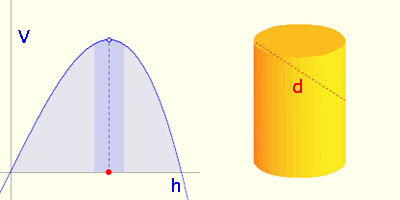
Kepler tabuló valores para reforzar su idea de que el volumen de esos cilindros con diagonales iguales cambian muy poco en un entorno de un máximo. (Baron, p. 116)
Esta página, y todo el libro, se puede consultar en The Posner Memorial Collection: Kepler, Nova Stereometria.
"Por lo tanto, mientras que si el método de los austriacos de determinar los precios fuera aplicado a los barriles renanos sería un claro fraude, aplicado a los barriles austriacos era bastante legítimo. La forma de los barriles austriacos tenía la ventaja de permitir ese método de medida tan simple y rápido. Kepler se quedó un poco más tranquilo". (Toeplitz, p. 83).
Esta fue, por lo tanto, una importantre contribución de Kepler: destacó que conforme nos aproximamos al valor máximo, el cambio en el volumen a partir de un determinado cambio en las dimensiones resultaba pequeño. Algunos años después, Fermat trabajó en este tipo de problemas de máximos y mínimos desde un punto de vista diferente.
El punto de vista de Fermat (que nació en 1601) fue diferente. En términos modernos, estaba interesado en la tangente a la curva y la relación entre la tangente y el máximo (o mínimo) de una función. Ferman fue el primero en resolver problemas de máximo-mínimo teniendo en cuenta el comportamiento característico de una función en sus valores extremos.
Las técnicas algebraicas de Fermat para abordar estos problemas puede verse actualmente como equivalente al estudio de la pendiente de la tangente a la curva que representa a la función. Newton y Leibniz tuvieron una idea todavía más clara y asociaron los máximos o mínimos con una tangente horizontal.
Usando nuestra terminología moderna, la interpretación geométrica de la derivada de una función en un punto es la pendiente de la tangente a la gráfica de la función en ese punto. Podemos ver intuitivamente que si f(x) es un máximo (o un mínimo) de una función diferenciable f entonces el valor de f cambia muy lentamente cerca de ese valor extremo.
Además, en los puntos más altos y más bajos de la gráfica de f la tangente es horizontal, es decir, su pendiente es 0: la derivada será 0 en los valores extremos.
Volviendo al problema de Kepler de las proporciones de un barril de vino, si V es el volumen del barril (como un cilindro) con un determinado valor de d fijo, entonces V es un polinomio en h y su derivada en fácil de calcular:
Si V alcanza un máximo, V' debe ser igual a 0, por lo tanto
Y este fue el resultado que Kepler encontró.
En el siguiente diagrama, la curva en azul es la gráfica de y=V(h) y la curva roja es el gráfica de In the diagram below, the blue curve is y=V'(h), de la derivada del volumen:
En resumen, lo que hemos querido mostrar aquí es cómo un problema práctico de medida del volumen de un barril de vino inspiró a Kepler para hacer importantes contribuciones en el desarrollo de el cálculo diferencial e integral.
Margaret E. Baron, The Origins of the infinitesimal Calculus, Dover Publications, New York, 1987.
Carl B. Boyer, The History of the Calculus and its Conceptual Development, Dover Publications, New York, 1959.
Roberto Cardil, Kepler: Doliometry, the volume of a barrel, y Kepler: Doliometría, el volumen de un tonel, matematicasVisuales, publicados el 8-9 December 2009.
Roberto Cardil, Kepler: el volumen de un tonel de vino, matematicasVisuales, publicados el 8 January 2010.
C.H. Edwards, The Historical Development of the Calculus, Springer-Verlag New York, 1979.
Felix Klein, Elementary Mathematics from an Advanced Standpoint. Arithmetic, Algebra, Analysis (p. 209), Dover Publications, New York, 2004.
Dirk J. Struik (ed.) , A Source Book in Mathematics, 1200-1800. Kepler. Integration Methods (pp. 192-197), Harvard University Press, Cambridge, MA, 1969.
Otto Toeplitz, The Calculus: A Genetic Approach (pp. 82-83), University Of Chicago Press, 1963.

|
Kepler en Mac Tutor History of Mathematics
Una biografía de Kepler. |

|
Versión original latina en The Posner Memorial Collection (libro completo)
Versión original en alemán en Convergence (dos páginas) Versiones originales de "Nova Stereometria" disponibles en la web. |

|
Kepler en matematicasVisuales - El área de un círculo
Kepler usó un enfoque infinitesimal intuitivo para calcular el área de un círculo. |

|
Kepler en Mathworld: Limón
Kepler en Mathworld: Manzana En Mathworld podemos ver varios sólidos de revolución definidos por Kepler. |

|
Archimedes' Method for Computing Areas and Volumes
Artículo de Gabriela Sanchis en Loci Convergence donde explica el método de Arquímedes basado en la Ley de la palanca. |

|
Arquímedes en matematicasVisuales - Área de un segmento parabólico
Arquímedes usó metodos infinitesimales intuitivos para descubrir áreas y volúmenes mil ochocientos años antes que Kepler y Cavalieri. |

|
The Sagacity of Circles: A History of the Isoperimetric Problem
Artículo de Jennifer Wiegert en Convergence. Resumen de la historia del problema de encontrar la región de mayor área con un perímetro dado. |

|
Thinking Outside the Box -- or Maybe Just About the Box
Artículo de David Meel y Thomas Hern en Convergence. Estudian el típico problema de la caja pero de un modo más complejo y realístico y nos muestran cómo puede ser usado para investigar optimización. |
Roberto Cardil Ricol es profesor en un instituto de enseñanza secundaria en España. Realizó estudios de Magisterio (Universidad de Huesca, España), es licenciado en Historia (Universidad de Barcelona, España) y en Matemáticas (Universidad de Zaragoza, España). Ha enseñado matemáticas a alumnos de todas las edades desde los seis años hasta la Universidad. Mantiene el sitio web www.matematicasvisuales.com y disfruta con la belleza de las Matemáticas.
Quiero agradecer a Janet Beery, editora de Convergence, por su apoyo y ánimo. Sin su ayuda este artículo no habría podido ser publicado.
Agradezo las sugestiones de 'referees' anónimos que mejoraron el artículo.
Gracias a The Posner Library por permitirme usar imágnes de su ejemplar del libro de Kepler "Nova stereometria doliorum vinariorum" en este artículo.
Miguel Cardil me ayudó en el diseño artístico de esta página y diseñó todos los elementos gráficos de los mathlets.
Quiero agradecer también a Kathleen Killorin su ayuda en la versión inglesa.