
Me parece muy interesante explorar los aspectos intuitivos de los orígenes del cálculo diferencial e integral. A pesar de las paradojas en las que fácilmente podremos caer si confiamos en la intuición cuando tratamos con procesos infinitos, este tipo de argumentos son muy sugerentes y forman parte de la Historia de las Matemáticas.
En el siglo XVII, abriendo nuevos caminos, podríamos decir que tanteando, casi a ciegas, trabajaron matemáticos como Kepler y Cavalieri, entre otros, con Arquímedes como un antecedente genial, mil ochocientos años antes.
Un ejemplo sencillo de este tipo de argumentos es considerar una circunferencia como un "polígono de infinitos lados" y obtener así la relación entre la longitud de la circunferencia y el área del círculo.
Podemos usar esta técnica para calcular el área de un sector circular, el área lateral de un cono o de un tronco de cono. También podemos extenderla, como hizo Kepler, para relacionar el área de la superficie esférica y el volumen de una esfera, considerando que la esfera esta formada por infinitos "conos infinitesimales" que tienen su vértice en el centro de la esfera y con sus bases cubren su superficie.
Para el cálculo de volúmenes dos enfoques diferentes son de especial interés. El principio de Cavalieri nos permite obtener volúmenes comparándolos con volúmenes conocidos.

También recordamos a Kepler al estudiar el "método de los discos" para calcular volúmenes de cuerpos de revolución.

El interés por el cálculo de áreas y volúmenes (asociado actualmente al cálculo integral) es muy anterior al estudio de la variación de una función, que implica conceptos mucho más modernos (relacionados con el concepto de derivada y el cálculo diferencial). Sin embargo, veremos que estas ideas, de un modo embrionario, ya están presentes en matemáticos como Kepler.
En esta página vamos a volver a tratar el asunto central del artículo Kepler: The Volume of a Wine Barrel publicado por Convergence (Revista digital de la Mathematical Association of America, Junio 2010). En ese artículo presenté varias aplicaciones interactivas en torno a la anecdota que llevó a Kepler al estudio de volúmenes de barriles y otros cuerpos y a escribir su libro (publicado en 1615) "Nova Stereometria doliorum vinariorum" (Nueva geometría sólida de los barriles de vino) donde usó técnicas infinitesimales que son antecedentes del cálculo diferencial e integral desarrollado por Newton y Leibnitz.
La siguiente página es una versión simplificada (siguiendo a Toeplitz):
Podemos ver el libro completo "Nova Stereometria doliorum vinariorum" en The Posner Library)
La anécdota que llevó a Kepler a escribir este libro es la siguiente: Cuando Kepler se casó por segunda vez en Linz compró un barril de vino para la boda. Para calcular el volumen del barril y el consiguiente precio del vino, el comerciante introdujo una vara por el agujero central del tonel hasta una de las tapas y con esa medida calculó el precio.
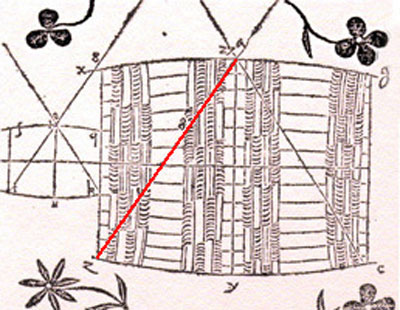
Este procedimiento sorprendió y enfadó a Kepler pues, dependiendo de la forma más o menos alargada del barril, una misma medida de la longitud de la varilla se corresponde con más o menos volumen de vino.
Esta anécdota animó a Kepler a estudiar el volumen de varios cuerpos, en particular, de cuerpos de revolución. En este tema, Kepler amplía un estudio que ya había sido tratado por los matemáticos griegos y que, actualmente, es estudiado por el cálculo integral.
Pero queriendo responder a la pregunta ¿tiene algún sentido el método del comerciante usado para medir el volumen de vino?, Kepler se plantea un problema de optimización que es un antecedente claro del trabajo de Fermat y que es un campo más novedoso en su época y que, actualmente, corresponde al estudio de la derivada de una función, es decir, al cálculo diferencial.
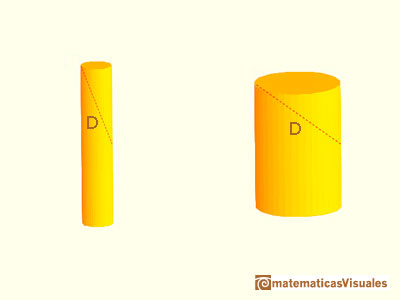
El problema es el siguiente: Dada una varilla de longitud D fija, la que usa el mercader para medir el volumen de vino, ¿qué dimensiones tiene un barril de modo que su volumen sea máximo?
Para empezar, Kepler simplifica el problema y lo estudia para cilindros (y prismas) y lo considera solo para medio barril. Entonces el problema quedaría así: Dada una diagonal D fija, ¿cuál es el mayor cilindro que tiene D como diagonal? ¿cuál es la razón entre el diámetro de la base y la altura de ese cilindro?

Kepler trata de comprender cómo cambia el volumen de los cilindros al considerar diferentes alturas.
Notamos que al ser D fijo todos estos cilindros están inscritos en una esfera con D como diámetro.
Para abordar este problema, Kepler estudia un caso particular y hace unos cálculos que resume en una tabla ("Praxis").
Esta es la página en la que Kepler escribe estos datos:

Podemos ver la tabla en detalle. Tiene tres columnas, las dos primeras son la altura y el diámetro de la base del cilindro:
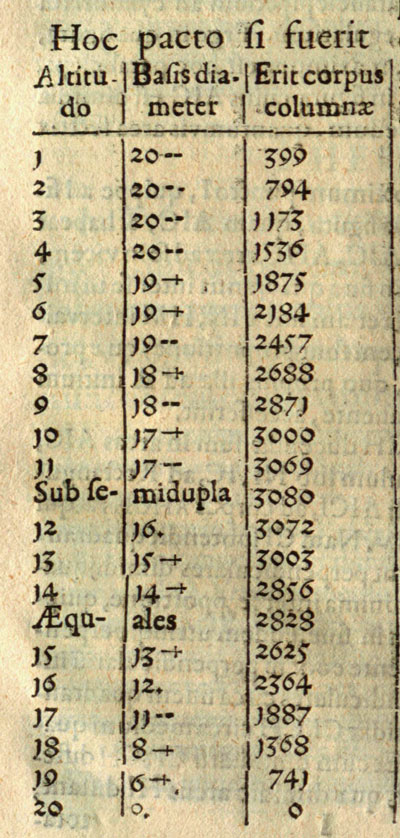
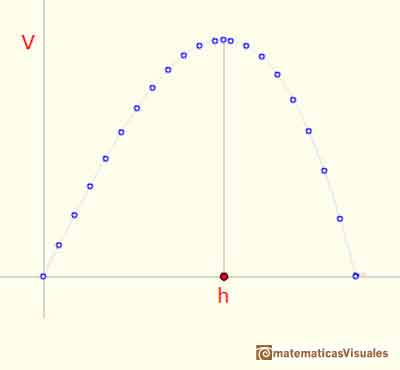
En la aplicación interactiva hay tres partes: abajo a la derecha está representado un cilindro con un prisma en su interior. Es el modelo geométrico que podemos rotar. A la izquierda está la tabla con los datos de Kepler. Si movemos el puntero arriba y abajo cambiamos el valor de la x en la gráfica que relaciona la altura h y el volumen V. El cilindro también modifica sus dimensiones. Moviendo a derecha e izquierda el valor de la altura en la gráfica también cambiamos la posición del cursor en la tabla y las dimensiones del cilindro.
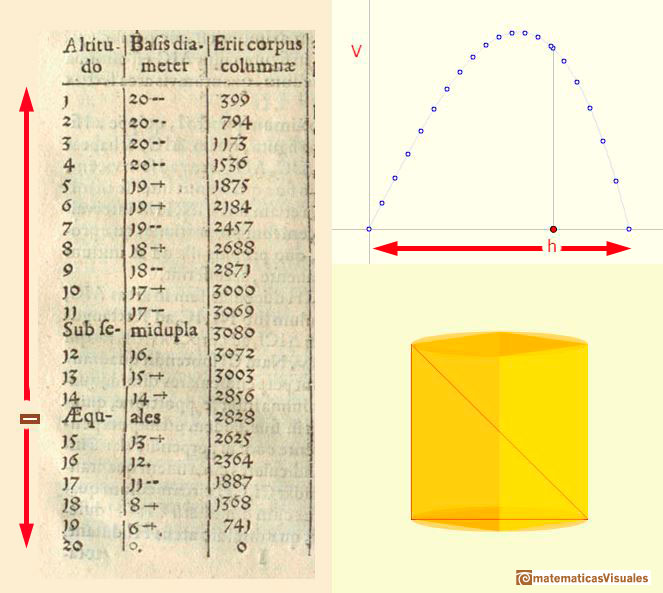
Kepler no dibujó un gráfico pero estaba interesado en el estudio de cómo cambia el volumen conforme cambia h. Esto lo hace con ayuda de la tabla de datos. Para nosotros el gráfico es un recurso que nos permite representar de un modo visual la relación entre dos variables. Estas representaciones gráficas son un poco posteriores a Kepler (Descartes, Fermat) y el concepto de función, con la generalidad que usamos actualmente, es mucho más moderna.
Mirando el gráfico sospechamos que hay un valor de la altura que nos da el máximo volumen. Es muy importante notar que alrededor de ese valor máximo el volumen cambia muy poco.
Kepler fue consciente de esto. Estas ideas fueron desarrolladas por Fermat, Leibniz y Newton.
Hemos comentado que Kepler se plantea un caso concreto, una valor de D. Mirando la tabla vamos a deducir ese valor y lo hacemos considerando los casos extremos:
Cuando h = 0:

Y si h = 20:


Entonces el valor de D es:
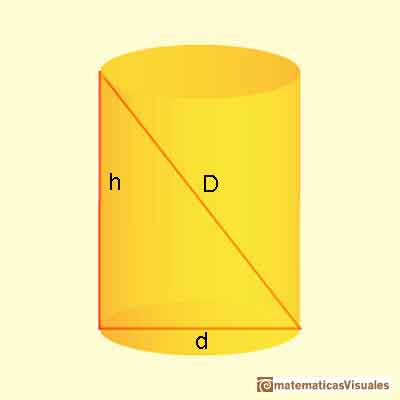
La segunda columna es el cálculo del valor del diámetro del cilindro (d) conforme cambia la altura. Es una aplicación del teorema de Pitágoras.

Podemos ver que Kepler solo aproxima el resultado poniendo + o - junto al valor. Veremos luego que el valor exacto no es realmente necesario para su objetivo, el cálculo de volúmenes. Con nuestros dispositivos modernos (calculadoras, hojas de cálculo) es muy fácil completar la tabla con valores más precisos y comparar nuestra tabla con los datos de Kepler.
Ahora vamos a ver la tercera columna. Esta columna está relacionada con el volumen pero vemos que no se corresponde con los volúmenes de los cilindros pues sabemos que los volúmenes de los cilindros se calculan usando el número pi (con sus infinitos decimales) y los números que usa Kepler son números naturales. Como Kepler quiere estudiar las variaciones de los volúmenes de los cilindros y para qué valor de la altura este volumen alcanza el máximo valor puede no tener en cuenta el factor pi, o cualquier otro factor, pues estos factores de proporcionalidad no modificaran la conclusión. Entonces Kepler lo que hace es estudiar un caso más simple, el del paralelepípedo de base cuadrada inscrito en una esfera. Es decir, Kepler va simplificando el problema: empieza estudiando barriles, luego cilindros y ahora prismas.
Si nos fijamos en el encabezamiento de la tercera columna, vemos que Kepler usa la palabra latina "columnae" (plural de "columna") para referirse al paralelepípedo de base cuadrada. Podemos traducir esta palabra por columna, pilar o poste.

Podemos deducir la fórmula que usó Kepler.
Recordamos que d es:
Primero calculamos el área de la base:
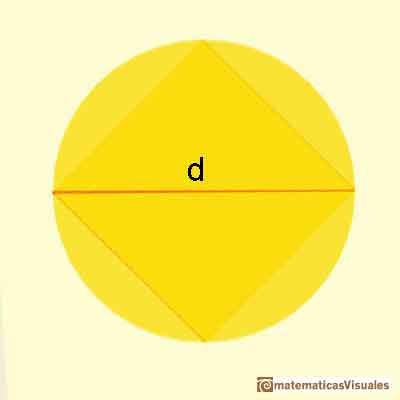
Ahora el volumen del poste:
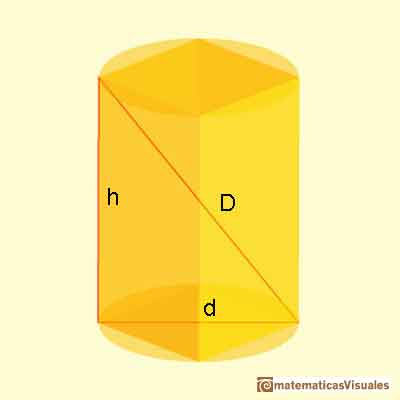
Kepler multiplica esta fórmula por dos pues el barril se medía insertando la varilla desde el centro del barril, es decir, el "barril" está simplificado a dos "postes".
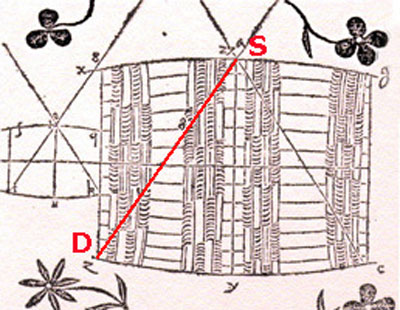
Es decir, que no hemos necesitado la segunda columna.
Podemos completar nuestra tabla y compararla con la de Kepler:
Kepler considera dos valores especiales. Uno está entre 14 y 15, con la palabra "Aequales". En este caso el diámetro de la base del cilindro (la diagonal de la base cuadrada) es igual a su altura:
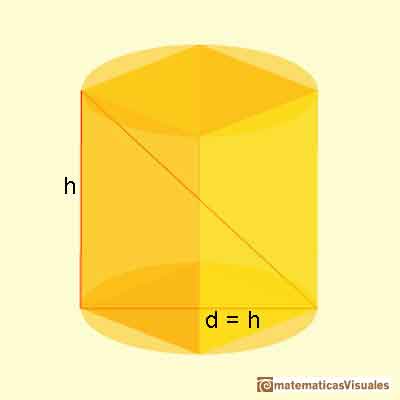
El valor de h=d es:
Y el volumen del poste si h=d is:

Vemos que este valor no se corresponde con un máximo:
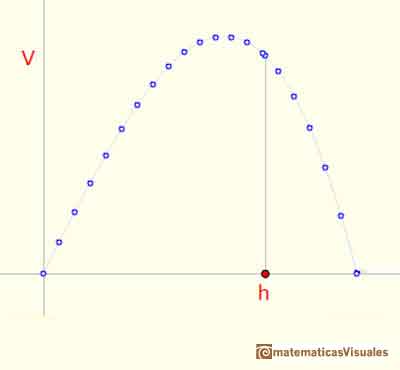
Cuando el cilindro tiene una altura igual a su diámetro su volumen no es máximo.

El segundo valor especial está entre 11 y 12 y Kepler escribe "Sub semidupla".
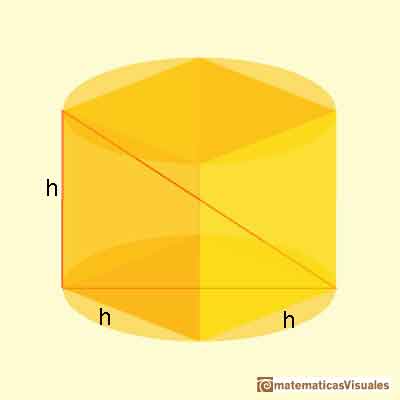
En este caso el volumen es máximo. El prisma es un cubo.
Podemos usar el teorema de Pitágoras otra vez y escribir:
La altura en este caso es:
Y el volumen es:
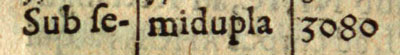
Este volumen es el máximo (¡esto tendría que probarse!. Siguiendo a Tikhomirov, pp. 50-53, podemos ver la demostración puramente geométrica de Kepler).

Después de esta "praxis", Kepler enuncia este resultado de maximización como su Teorema IV de la segunda parte:

"Teorema IV. De todos los paralelepípedos rectángulos de base cuadrada inscritos en una esfera, el de mayor volumen es el cubo."
Uno de los resultados principales de su libro es el teorema V de la segunda parte:

"Teorema V. De todos los cilindros con la misma diagonal, el mayor y más voluminoso es aquel en el que la razón del diámetro de la base y su altura es la raíz cuadrada de dos."
Kepler usa la palabra "semidupla" y podemos sospechar el significado de esta palabra:
Este teorema es la solución del problema que planteábamos al principio: inscribir en una esfera dada un cilindro de volumen máximo.
Este resultado se deduce del teorema IV pues el volumen de un cilindro es:
Es decir:
Entonces el volumen del cilindro de mayor volumen tiene inscrito un cubo que es el prisma más voluminoso en esas condiciones.
Si pensamos en el barril de volumen máximo, teniendo en cuenta que la vara se introduce por el centro, entonces su modelo simplificado sería un cilindro de doble altura que contiene dos cubos.
Entonces la altura de este barril máximo será la raíz cuadrada de dos por el diámetro, o lo que es lo mismo, la altura tiene que ser dos veces la raíz cuadrada de dos por el radio. Aproximadamente podemos decir, como hace Kepler, que un tonel cuya altura sea tres veces el radio de la base tiene el volumen máximo en esas condiciones.
Notamos que esa es justamente la relación de la línea de la tabla que corresponde con la altura 12 (que hay que multiplicar por dos, es decir, veinticuatro) y el diámetro 16. Valores que no son el máximo pero muy cercanos.
Esta era la proporción típica de los barriles austríacos, es decir, el tipo de barril para el que el comerciante aplicó su método de medir el volumen con una vara. En la zona de origen de Kepler, al oeste de Alemania, en la zona del Rhin, los barriles solían ser más alargados.
Después de probar el teorema, Kepler escribe una conclusión muy interesante:

"A partir de aquí está claro que, los constructores de barriles de Austria, guiados por el sentido común y geométrico, cuando hacen un barril, toman el radio de la base un tercio la longitud de la duela. Cuando se hace esto, el cilindro que construimos mentalmente entre las dos bases está formado por dos mitades, cada una de las cuales está próxima a las condiciones del teorema V y tendrá, por lo tanto, una capacidad máxima incluso si nos desviamos un poco de las reglas exactas cuando se construye el tonel, porque los valores próximos al óptimo cambian la capacidad muy poco... Eso es así porque cerca de un máximo los decrecimientos por ambos lados al principio son solo imperceptibles." (Traducción del inglés del libro de Tikhomirov).
Es decir, que el método que usó el mercader de vinos podría considerarse aceptable pues se aplicaba a un barril austríaco. Sin embargo, no sería adecuado para los barriles renanos, más alargados, pues sería mucho menos preciso.
"Esta conclusión de Kepler contienen el algoritmo fundamental para encontrar valores máximos que fue posteriormente perfeccionado en un teorema exacto. Primero fue descrito (para polinomios) por Fermat (1629) y, después, en una forma general, por Newton y Leibniz (Tikhomirov)
Este teorema de Fermat nos da una condición necesaria para los máximos y mínimos locales de una función: si una función tiene un máximo o un mínimo local para un determinado valor y la función es derivable en ese punto, entonces su derivada es nula. Geométricamente, decimos que la tangente a la gráfica en ese punto es horizontal.
REFERENCIAS
 SIGUIENTE
SIGUIENTE
MÁS ENLACES




















 ANTERIOR
ANTERIOR