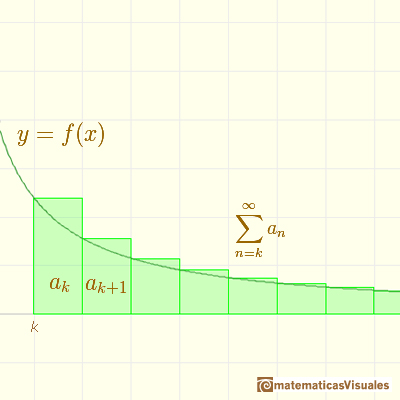
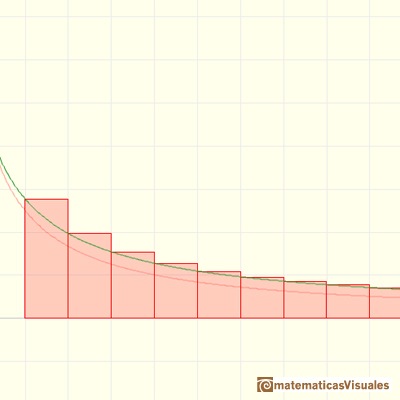
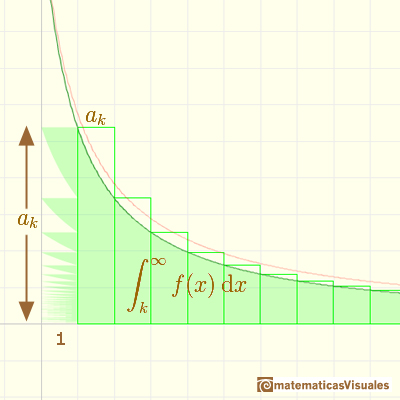
If we start with a decreasing and positive function
You can define
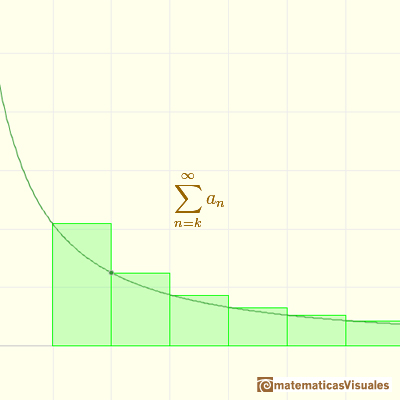
And then you get a series of positive terms
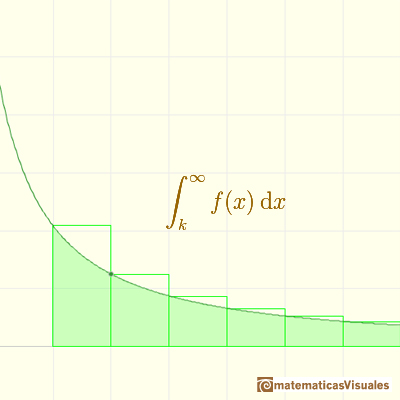
In general, you can say that this inequality holds:
In the mathlet you can play with a particular case
Dragging the dots you can change the values of lambda and p.
In theses cases, the series that you get is like a p-series (translated and expanded).
For example, consider the integral
Then
The series converges and the lower and upper bounds are
MORE LINKS

One intuitive example of how to sum a geometric series. A geometric series of ratio less than 1 is convergent.

The geometric series of ratio 1/2 is convergent. We can represent this series using a rectangle and cut it in half successively. Here we use a rectangle such us all rectangles are similar.
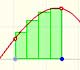
The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.
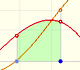
If we consider the lower limit of integration a as fixed and if we can calculate the integral for different values of the upper limit of integration b then we can define a new function: an indefinite integral of f.
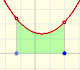
To calculate the area under a parabola is more difficult than to calculate the area under a linear function. We show how to approximate this area using rectangles and that the integral function of a polynomial of degree 2 is a polynomial of degree 3.
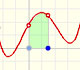
We can see some basic concepts about integration applied to a general polynomial function. Integral functions of polynomial functions are polynomial functions with one degree more than the original function.
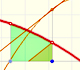
The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.
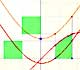
The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).

By increasing the degree, Taylor polynomial approximates the exponential function more and more.
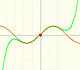
By increasing the degree, Taylor polynomial approximates the sine function more and more.
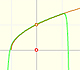
The function is not defined for values less than -1. Taylor polynomials about the origin approximates the function between -1 and 1.
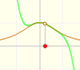
This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

A complex polinomial of degree 3 has three roots or zeros.

Every complex polynomial of degree n has n zeros or roots.
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

The Complex Cosine Function maps horizontal lines to confocal ellipses.
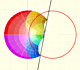
Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.

The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
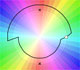
Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

The power series of the Cosine Function converges everywhere in the complex plane.

We will see how Taylor polynomials approximate the function inside its circle of convergence.

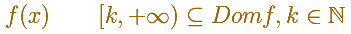
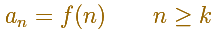
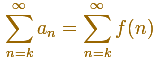
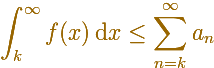
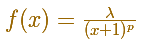
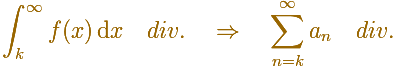
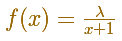
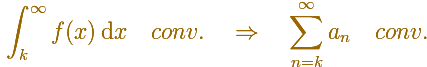
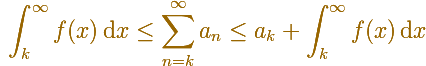
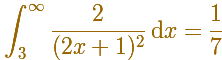
 NEXT
NEXT
 PREVIOUS
PREVIOUS






































