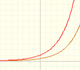
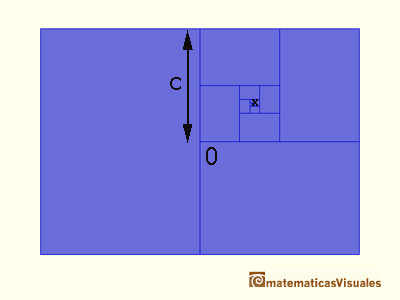
We have already seen, studying the geometric series of ratio 1/4, that
a geometric series
is a convergent series when the ratio is less than 1. Its sum is:
A simple case is when the ratio is
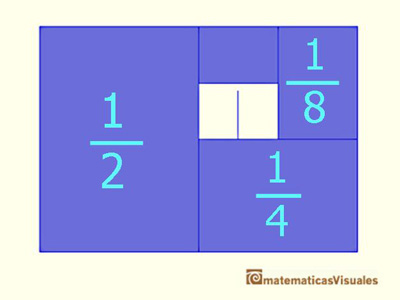
Then, the geometric series we want to add can be represented in this way:
The sum of the geometric series of ratio 1/2 is:
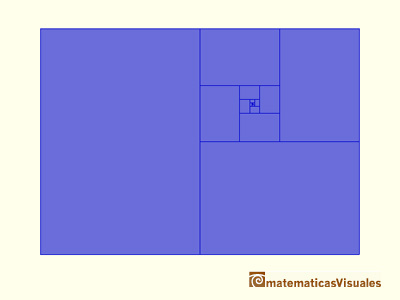
In this visualization we have used a rectangle with a particular shape: when we cut it in half we get two
rectangles with the same shape. This aspect ratio is used, for example, in the international papel size standard,
ISO 216 (based on the German DIN, for example, DIN A4).
The aspect ratio of these rectangles is:
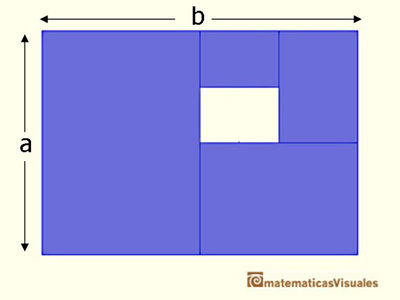
In the animation, these rectangles follow a kind of spiral around a point.
¿Can you think what are its coordinates? The result is related with another geometric series:
the geometric series of ratio 1/4.
MORE LINKS
Geometric sequences graphic representations. Sum of terms of a geometric sequence and geometric series.
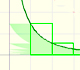
Using a decreasing positive function you can define series. The integral test is a tool to decide if a series converges o diverges. If a series converges, the integral test provide us lower and upper bounds.
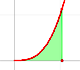
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
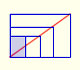
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
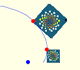
A Dilative Rotation is a combination of a rotation an a dilatation from the same point.

In an equiangular spiral the angle between the position vector and the tangent is constant.
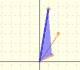
We can see it as a dilatative rotation.
The multiplication by a complex number is a transformation of the complex plane: dilative rotation.

From a complex number we can obtain a geometric progression obtaining the powers of natural exponent (multiplying successively)

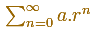
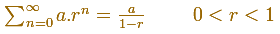
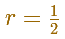
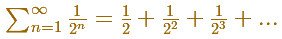
 NEXT
NEXT
 PREVIOUS
PREVIOUS