|
|
|
Sum of a Geometric Series
It is important to try to sum a geometric series.
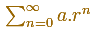
When the ratio is bigger than 1 the general term get bigger and bigger and the series do not converge.
When the ratio is less than 1, this series converge and its sum is:
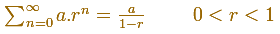
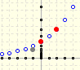
Here we are going to study a particular case, when the ratio is:
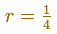
Then, this series can be represented in this manner:
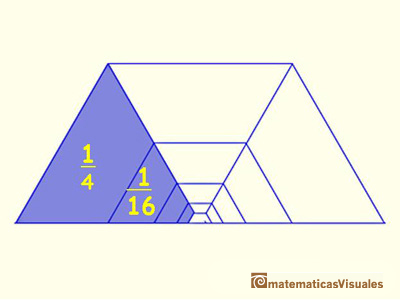
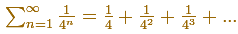
Then, the sum of this geometric series of ration 1/4 is:
NEXT
The geometric series of ratio 1/2 is convergent. We can represent this series using a rectangle and cut it in half successively. Here we use a rectangle such us all rectangles are similar.
PREVIOUS
Geometric sequences graphic representations. Sum of terms of a geometric sequence and geometric series.
MORE LINKS
We can study several properties of exponential functions, their derivatives and an introduction to the number e.
Using a decreasing positive function you can define series. The integral test is a tool to decide if a series converges o diverges. If a series converges, the integral test provide us lower and upper bounds.
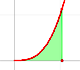
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
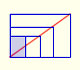
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
A Dilative Rotation is a combination of a rotation an a dilatation from the same point.
In an equiangular spiral the angle between the position vector and the tangent is constant.
The multiplication by a complex number is a transformation of the complex plane: dilative rotation.
From a complex number we can obtain a geometric progression obtaining the powers of natural exponent (multiplying successively)