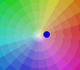
|
|
|
Complex Numbers: Geometric Progressions
Las progresiones geométricas complejas están relacionadas con
* la multiplicación de números complejos
* la rotación dilatativa
* espirales equiangulares
Estas tres ideas han sido estudiadas en otras páginas de matematicasVisuales.
En el siguiente applet podemos jugar con la misma idea con puntos coloreados (pudiendo controlar el radio de esos puntos)
En la siguiente animación podemos ver la rotación dilatativa que relaciona cada punto con el siguiente y la relación con la espiral equiangular:
Una animación análoga con colores
En el siguiente applet exploramos sub-progresiones de una progresión geomérica:
LINKS
The multiplication by a complex number is a transformation of the complex plane: dilative rotation.
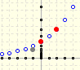
Geometric sequences graphic representations. Sum of terms of a geometric sequence and geometric series.
In an equiangular spiral the angle between the position vector and the tangent is constant.