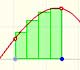
Which bounded functions are integrable?
This is a difficult question to answer. One simple partial answer is that monotonic functions are integrable.
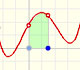
A function is monotonic on an interval if it is either increasing or decreasing on the interval. If f is a monotonic function on [a,b] then it is bounded and integrable. (And the result can be easily generalized to bounded piecewise monotonic functions [see Ross, p. 196]).
"Fortunately, most of the functions that occur in practice are monotonic or sums of monotonic functions, so the result of this miniature theory of integration is quite comprehensive." (Apostol, p. 76)
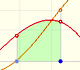
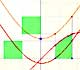
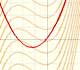
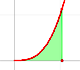
In the applet you can play with a simple case of monotonic functions: continuous monotonic functions, but the result is true in general. (By the way, another important family of integrable functions are all continuous functions on [a,b]).
In the applet it is possible to modify the curve and the ends of integration, to increase or to diminish the number of rectangles, to show the error we make and a bound of that error. We can see an animation about that.
Before considering the theoretical aspect of the problem we can think a little about the approximation of the value of the definite integral of a monotonic function.
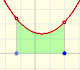
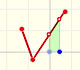
When approximating an integral using rectangles we make an error. In some cases, for example, in monotonic functions, we can limit the magnitude of the error. The error is equal to the sum of the areas of the blue "curved triangles".
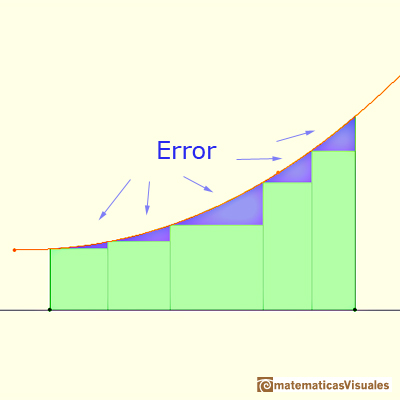
This error is less than the area of a rectangle.
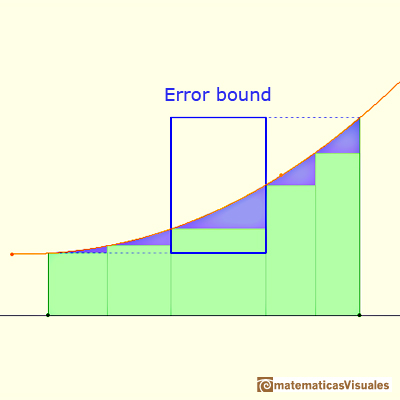
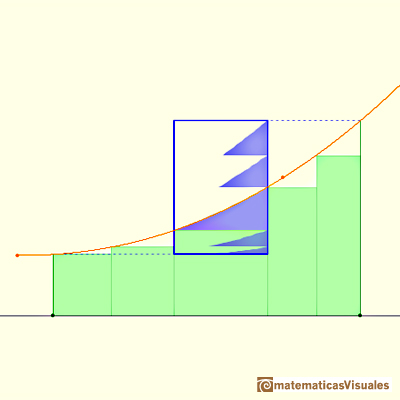
If we consider a simple case, when the bases of the rectangles are equal, then we can calculate an error bound:
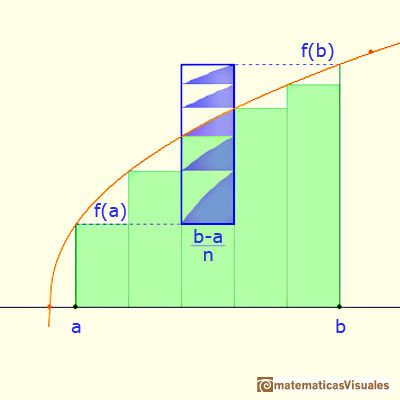
Using refined partitions we obtain as small bounds of the error as we want. Because when we refine a partition the base of the rectangle is smaller.
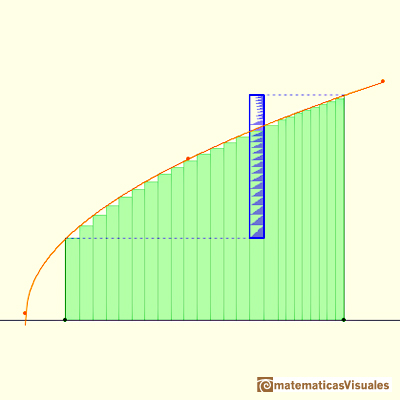
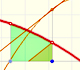
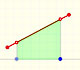
Now we are going to prove that a monotonic positive increasing function on [a,b] is integrable.
We start with a partition of the interval:
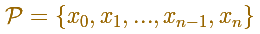
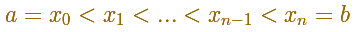
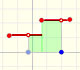
If we divide the interval into n equal parts then the width of each rectangle is:
We can calculate an upper bound of the integral:
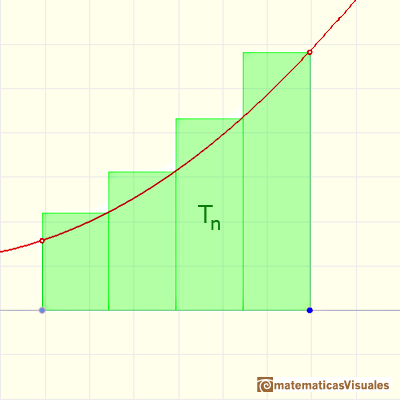
We consider the decreasing sequence
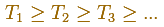
With the same partition, this is a lower bound of the integral:
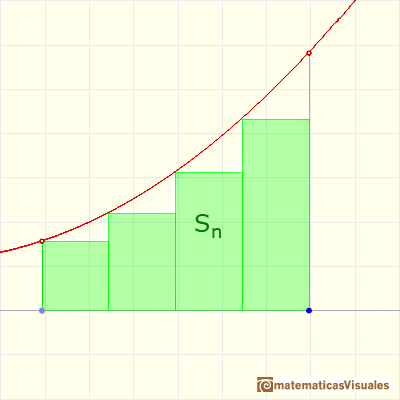
We consider the increasing sequence
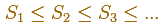
If this two sequences converge toward one and the same limit, we can call this limit the definite integral, and write
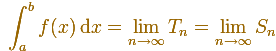
But the question always is whether they do converge.
When we consider an increasing monotonic function we have an increasing sequence (Sn) and a decreasing sequence (Tn). Then the question is only whether we can verify
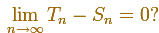
We can calculate Tn - Sn
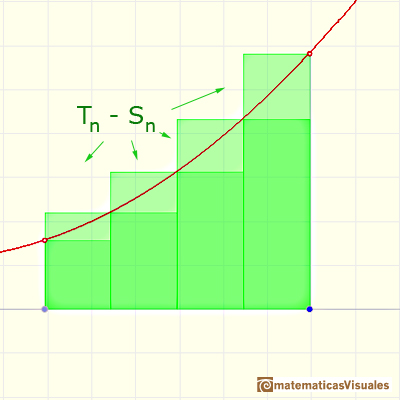
Then the limit
We conclude that if f is monotonic in the interval [a,b], then the definite integral exists. [Toeplitz, p.64]
![Definite integral of monotonic functions: if f is monotonic in the interval [a,b], then the definite integral exists | matematicasVisuales](../../../../images/analysis/integral/integralCota/formula/integralCota7.gif)
This is Newton's approach to the question in 'The Mathematical Principles of Natural Philosophy' ('Principia'). You can read this book in Google books (p. 17), California Digital Library or a latin version in Cambridge Digital Library, for example.

REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS