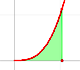
We have already seen how to define a definite integral.
Suppose now that f is integrable on [a,b]. We shall keep a and f fixed, then can define a new function on [a,b] by
This is called an indefinite integral.
If f is positive, F(x) is sometimes called an Area function.
We say an indefinite integral rather than the indefinite integral because F also depends on the lower limit a.
Different values of a will lead to different functions F. But the difference between two integral functions of the same function is
independent of x, they differ only by a constant. [Apostol]
We can see a very similar behavior when we study the antiderivative concept.
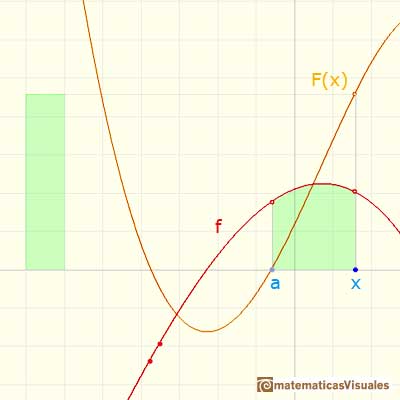
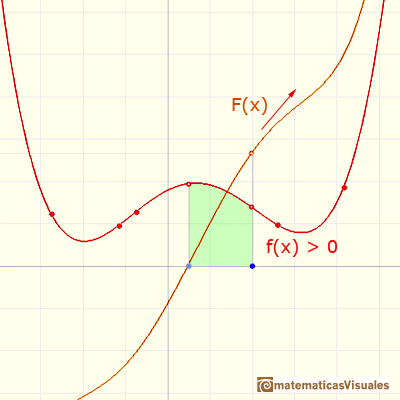
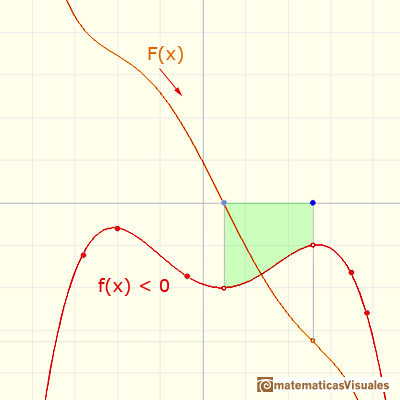
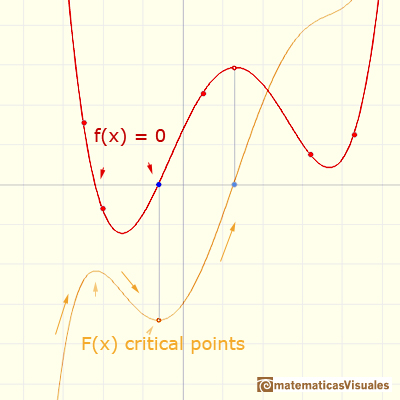
If f is positive in an interval, then F (in this case F is area) is increasing.
If f is negative in an interval, then F is decreasing.
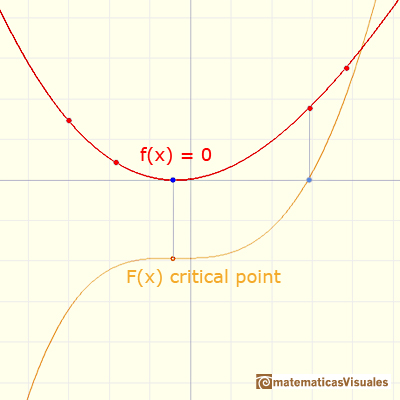
If f(x)=0 then x is a critical point of F.
This three relationships between F and f are precisely those enjoyed by a function and its derivative.
We can start studying integrals using simple polynomial functions:
linear, quadratic and
general polynomial functions.
REFERENCES
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc.
Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc.
MORE LINKS
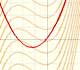
If the derivative of F(x) is f(x), then we say that an indefinite integral of f(x) with respect to x is F(x). We also say that F is an antiderivative or a primitive function of f.
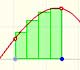
The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.
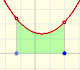
To calculate the area under a parabola is more difficult than to calculate the area under a linear function. We show how to approximate this area using rectangles and that the integral function of a polynomial of degree 2 is a polynomial of degree 3.
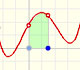
We can see some basic concepts about integration applied to a general polynomial function. Integral functions of polynomial functions are polynomial functions with one degree more than the original function.
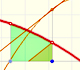
The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.
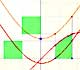
The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).
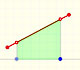
As an introduction to Piecewise Linear Functions we study linear functions restricted to an open interval: their graphs are like segments.
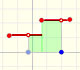
A piecewise function is a function that is defined by several subfunctions. If each piece is a constant function then the piecewise function is called Piecewise constant function or Step function.
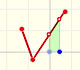
A continuous piecewise linear function is defined by several segments or rays connected, without jumps between them.
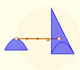
Archimedes show us in 'The Method' how to use the lever law to discover the area of a parabolic segment.

In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. We can see an intuitive approach to Archimedes' ideas.
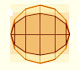
In his book 'On Conoids and Spheroids', Archimedes calculated the area of an ellipse. It si a good example of a rigorous proof using a double reductio ad absurdum.

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.

Kepler was one mathematician who contributed to the origin of integral calculus. He used infinitesimal techniques for calculating areas and volumes.

Studying the volume of a barrel, Kepler solved a problem about maxima in 1615.

Using Cavalieri's Principle we can calculate the volume of a sphere.

Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.

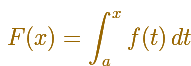
 NEXT
NEXT
 PREVIOUS
PREVIOUS