The logarithm of the number e is equal to 1. It is to say (and we can consider this as a definition of number e)
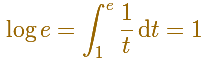
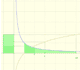
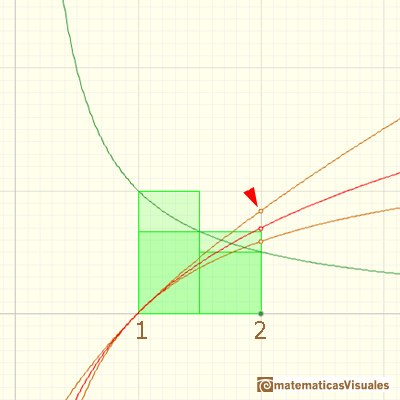
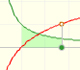
In the applet you can see two logarithm function approximations. We use partitions with a variable number of rectangles and we can be as accurate as we want.
Basis of all rectangles are equal. One approximations is by excess and the other is by defect.
How many rectangles you need to be sure that log2 is less than 1?
It is easy to see that log4 is bigger than 1: 3 rectangles are enough.
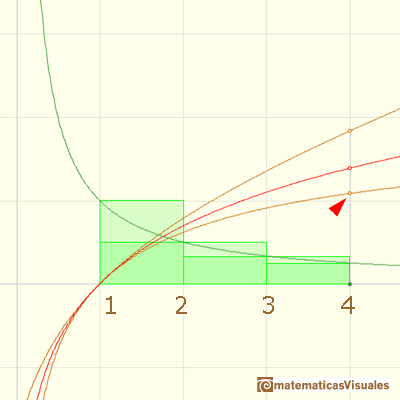
Then we can say that
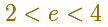
Are they enough 6 rectangles to be sure that log3 is bigger than 1? No, and you can see this zooming.
But using 7 rectangles you can be sure.
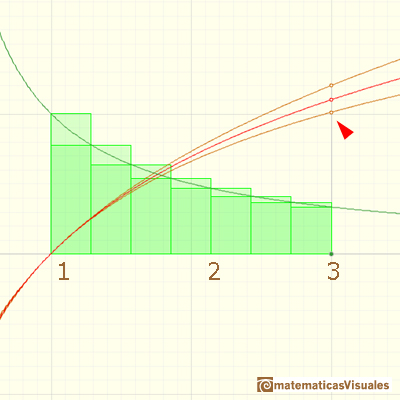
Then we can say that
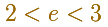
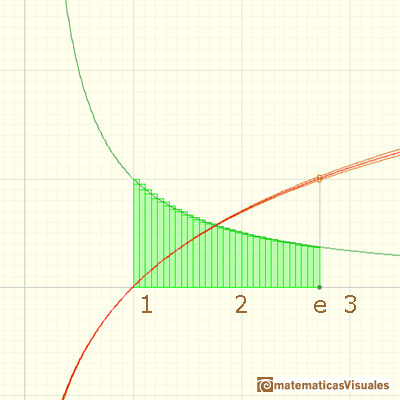
Using more and more rectangles you can get better approximations of number e.
The value of number e is approximately
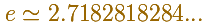
There are better ways to calculate the value of e but these are good exercises to understand the definition of e
as an integral.
By increasing the degree, Taylor polynomial approximates the exponential function more and more.
REFERENCES
A. I. Markushevich, Areas and Logarithms, D.C. Heath and Company, 1963.
Serge Lang, A First Course in Calculus, Third Edition, Addison-Wesley Publishing Company.
Tom M. Apostol, Calculus, Second Edition, John Willey and Sons, Inc.
Michael Spivak, Calculus, Third Edition, Publish-or-Perish, Inc.
Otto Toeplitz, The Calculus, a genetic approach, The University of Chicago Press, 1963.
Kenneth A. Ross, Elementary Analysis: The Theory of Calculus, Springer-Verlag New York Inc., 1980.
MORE LINKS
We can study several properties of exponential functions, their derivatives and an introduction to the number e.
Using the integral of the equilateral hyperbola we can define a new function that is the natural logarithm function.
The natural logaritm can be defined using the integral of the rectangular hiperbola. In this page we are going to see an important property of this integral. Using this property you can justify that the logarithm of a product is the sum of the logarithms.
After the definition of the natural logarithm function as an integral you can define the exponential function as the inverse function of the logarithm.
Different hyperbolas allow us to define different logarithms functions and their inversas, exponentials functions.
Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.
By increasing the degree, Taylor polynomial approximates the exponential function more and more.
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
The complex exponential function is periodic. His power series converges everywhere in the complex plane.
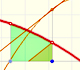
The Fundamental Theorem of Calculus tell us that every continuous function has an antiderivative and shows how to construct one using the integral.
The Second Fundamental Theorem of Calculus is a powerful tool for evaluating definite integral (if we know an antiderivative of the function).
As an introduction to Piecewise Linear Functions we study linear functions restricted to an open interval: their graphs are like segments.
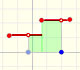
A piecewise function is a function that is defined by several subfunctions. If each piece is a constant function then the piecewise function is called Piecewise constant function or Step function.
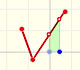
A continuous piecewise linear function is defined by several segments or rays connected, without jumps between them.
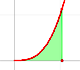
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
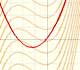
If the derivative of F(x) is f(x), then we say that an indefinite integral of f(x) with respect to x is F(x). We also say that F is an antiderivative or a primitive function of f.
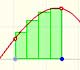
The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.
Monotonic functions in a closed interval are integrable. In these cases we can bound the error we make when approximating the integral using rectangles.
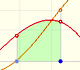
If we consider the lower limit of integration a as fixed and if we can calculate the integral for different values of the upper limit of integration b then we can define a new function: an indefinite integral of f.
We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.
NEXT
PREVIOUS
