We have already study the end behavior of several rational functions.
If the degree of the numerator is less than the degree of the numerator, the rational function has a horizontal asymptote y=0;
If the degree of the numerator is equal than the degree of the numerator, the rational function has a horizontal asymptote y=k;
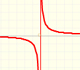
Rational functions can be writen as the quotient of two polynomials. Linear rational functions are the simplest of this kind of functions.
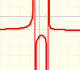
When the denominator of a rational function has degree 2 the function can have two, one or none real singularities.
If the degree of the numerator is exactly one more than the degree of the numerator, the rational function has a oblique or slant asymptote.
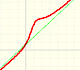
For large absolute values of x, some rational functions behave like an oblique straight line, we call this line an oblique or slant asymptote.
If you divide the numerator of a rational function by its denominator you get a polynomial quotient Q(x) plus a remainder term whose
degree is less than of the denominator. The remainder, when divided by the denominator, contributes very little to the y-values fo the
rational function for large values of |x|.
We say that the rational function is asymptotic to the polynomial quotient. The end behavior
of the rational function follow the end behavior of the polynomial quotient. f(x) will behave like Q(x) for large values of x.
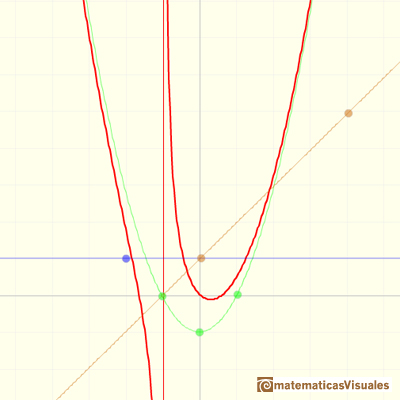
We can start with a rational function that has a polynomial of degree 2 as a polynomial quotient, a number as a remainder and
a degree 1 polynomial as a denominator.
In the first mahtlet you could play with the three elements of this kind of rational function:
a quotient polynomial (in green, a parabola), the numerator (a number, in blue a horizontal line) and
the denominator (a straight line, in orange)
For example:
The formula for the previous graph is:
The equation of the quotient polynomial (asymptotic function) is:
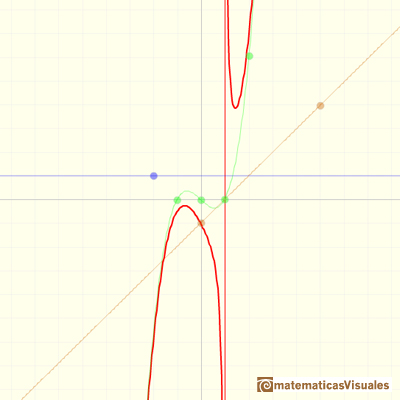
Another example:
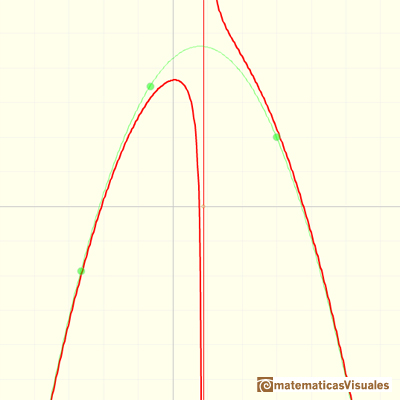
In the next video we are going to explore rational functions that has a degree 3 polynomial
as a polynomial quotient, a number as a remainder and a degree 1 polynomial as a denominator.
The three elements of this kind of rational function are:
a quotient polynomial (in green, a cubic function), the numerator (a number, in blue a horizontal line) and
the denominator (a straight line, in orange)
For example:
The formula for the previous graph is:
The equation of the quotient polynomial (asymptotic function) is:
Another example:
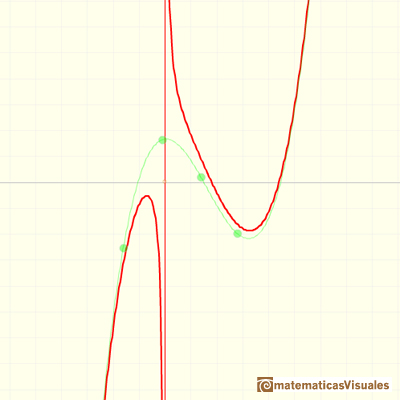
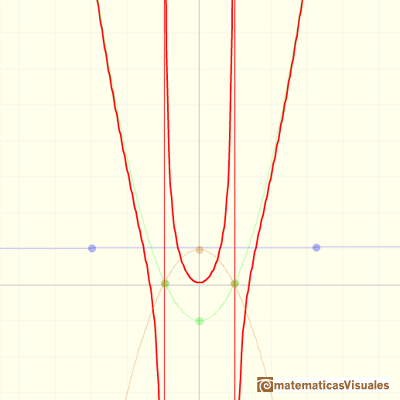
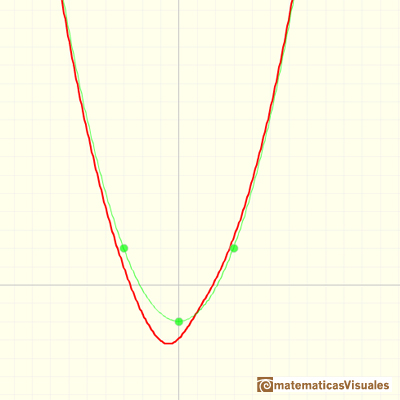
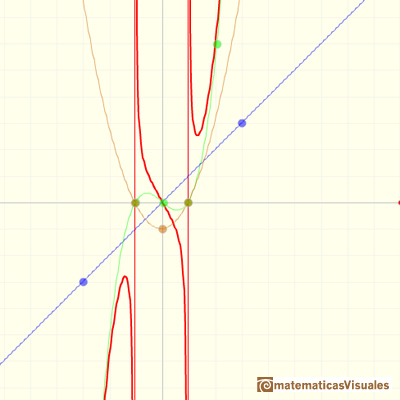
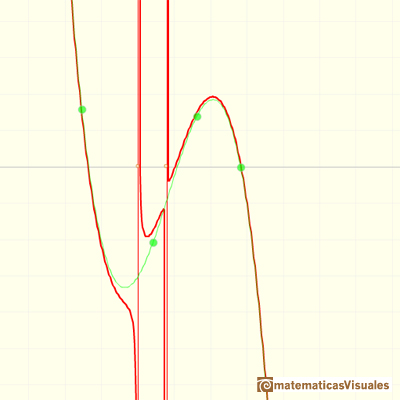
In the last video of this series we are going to see rational functions that has a degree 3 polynomial
as a polynomial quotient, a degree 1 polynomial as a remainder and a degree 2 polynomial as a denominator.
REFERENCES
G.E. Shilov, Calculus of Rational Functions, Mir Publishers, Moscow.
I.M. Gelfand, E.G. Glagoleva, E.E. Shnol, Functions and Graphs, Dover Publications, Inc., Mineola, New York.
MORE LINKS

Rational functions can be writen as the quotient of two polynomials. Linear rational functions are the simplest of this kind of functions.

When the denominator of a rational function has degree 2 the function can have two, one or none real singularities.
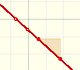
Two points determine a stright line. As a function we call it a linear function. We can see the slope of a line and how we can get the equation of a line through two points. We study also the x-intercept and the y-intercept of a linear equation.
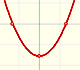
Polynomials of degree 2 are quadratic functions. Their graphs are parabolas. To find the x-intercepts we have to solve a quadratic equation. The vertex of a parabola is a maximum of minimum of the function.
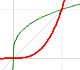
Power with natural exponents are simple and important functions. Their inverse functions are power with rational exponents (a radical or a nth root)
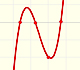
Polynomials of degree 3 are cubic functions. A real cubic function always crosses the x-axis at least once.
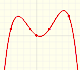
We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.
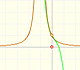
The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.
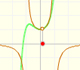
This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.
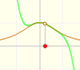
This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

We will see how Taylor polynomials approximate the function inside its circle of convergence.

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

A complex polinomial of degree 3 has three roots or zeros.

Every complex polynomial of degree n has n zeros or roots.
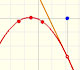
The derivative of a quadratic function is a linear function, it is to say, a straight line.
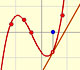
The derivative of a cubic function is a quadratic function, a parabola.
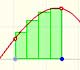
The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.




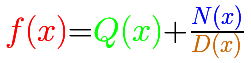
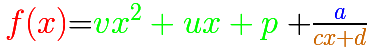
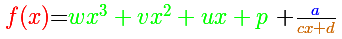
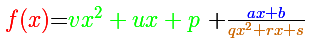
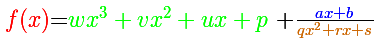
 PREVIOUS
PREVIOUS


























 NEXT
NEXT






