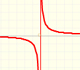
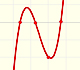
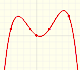
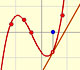
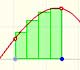
In this page we are going to study deeply the end behavior of rational functions. It is to say how it is the function for large |x| (x positive or negative) or how the function behaves when 'x tends to infinity' (positive or negative).

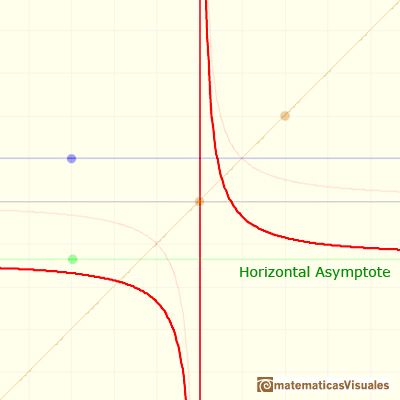
We have already seen that when the degree of the denominator is bigger than the degree of the numerator (Proper rational functions) then the rational function has a horizontal asymptote y = 0 (the x-axis). For example, this is the case of the equilateral hyperbola.

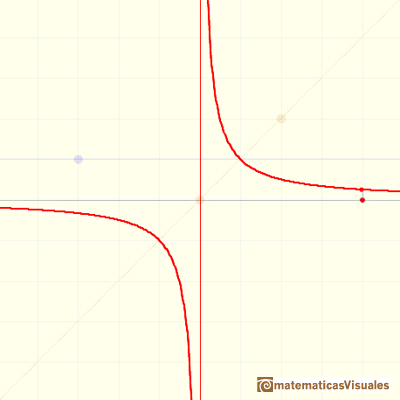
If the degree of the numerator is equal or bigger than of the denominator this rational function is improper. You can divide the numerator of a rational function by its denominator and get a polynomial quotient plus a polynomial remainder term whose degree is less than of the denominator. The remainder divided by the denominator is a Proper rational function and contributes very little to the y-values of the rational function for large |x|.

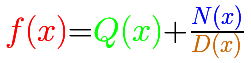
We have already seen several examples of Improper rational functions but only when the degree of the denominator is equal than the degree of the numerator. In those cases, if you divide you get a quotient that is a number. Then you can write the rational function as a number plus a proper rational function.

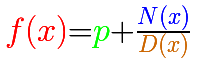
With that number (that you can calculate dividing only the leadings terms of the numerator and denominator) you can write the horizontal asymptote (an horizontal straight line, a constant function).

This is the equation of the horizontal asymptote:

When the degree of the numerator is higher than the degree of the denominator there is no horizontal asymptote.

In this page we are going to study the case when the degree of the numerator is greater than the degree of the denominator but it is greater only by one.

As before, you can divide numerator by denominator and, using the quotient and the remainder, you can write the rational function as a polynomial plus a proper rational function. In this cases, this polynomial is a degree 1 polynomial. This straight line controls the behavior of the rational function when the module of x is big (then the proper rational function is very small).

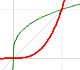
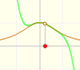
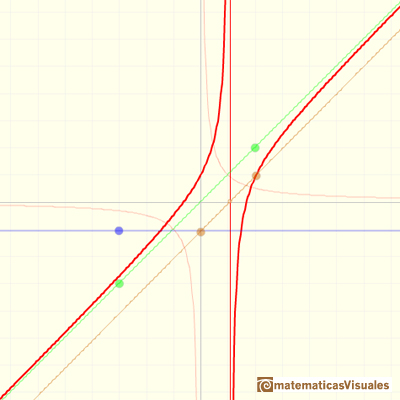
The quotient polynomial Q(x) is linear, Q(x)=ax+b, then y=ax+b is called an slant or oblique asymptote for f(x).

If the degree of the numerator is exactly one more than the degree of the denominator, the end behavior of this rational function is like an oblique linear function. The graph of the rational function attempts to imitate an oblique straight line in the domain's positive or negative extremes. In these cases we say that the rational function has an oblique (or slant) asymptote.

The first case is when the numerator has degree 2 and the denominator has degree 1:

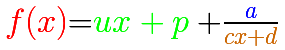
In this case, this is the equation of the oblique asymptote:

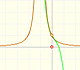
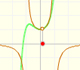
In the first mahtlet you could play with the three elements of this kind of rational function: a degree 1 polynomial (in green, a straight line), the numerator (a number, in blue a horizontal line) and the denominator (a straight line, in orange)

For example:

The formula for the previous graph is:

In this case, this is the equation of the oblique asymptote:

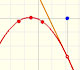
Another example:

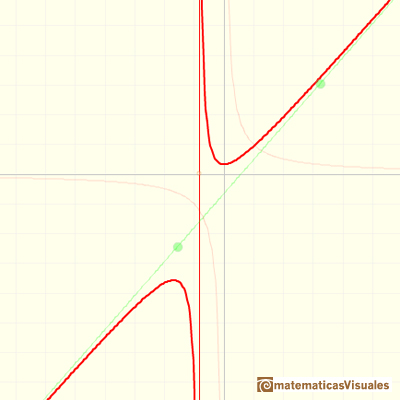
In the next mathlet you can play with rational functions that has a degree 3 polynomial in the numerator and the denominator has degree 2.

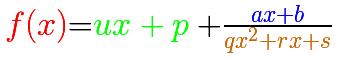
As before, the equation of the oblique asymptote is:

The three elements of this kind of rational function are: a degree 1 polynomial (in green, a straight line), the numerator (in blue, a straight line) and the denominator (a parabola, in orange):

For example:

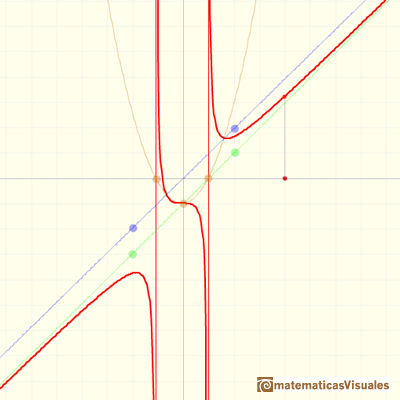
The formula for the previous graph is:

The equation of the oblique asymptote is:

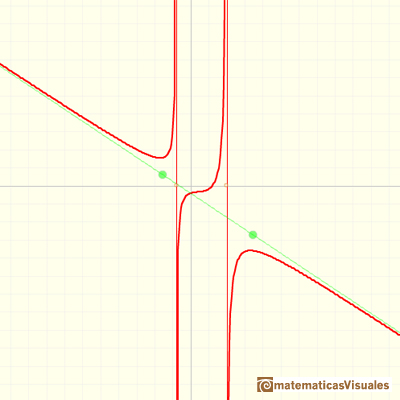
Another example:

MORE LINKS

Rational Functions (1): Linear rational functions

Rational functions can be writen as the quotient of two polynomials. Linear rational functions are the simplest of this kind of functions.

Polynomial Functions (1): Linear functions

Two points determine a stright line. As a function we call it a linear function. We can see the slope of a line and how we can get the equation of a line through two points. We study also the x-intercept and the y-intercept of a linear equation.

Polynomial Functions (2): Quadratic functions

Polynomials of degree 2 are quadratic functions. Their graphs are parabolas. To find the x-intercepts we have to solve a quadratic equation. The vertex of a parabola is a maximum of minimum of the function.

Powers with natural exponents (and positive rational exponents)

Power with natural exponents are simple and important functions. Their inverse functions are power with rational exponents (a radical or a nth root)

Polynomial Functions (3): Cubic functions

Polynomials of degree 3 are cubic functions. A real cubic function always crosses the x-axis at least once.

Polynomial Functions (4): Lagrange interpolating polynomial

We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.

Taylor polynomials (4): Rational function 1

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (5): Rational function 2

The function has a singularity at -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Taylor polynomials (6): Rational function with two real singularities

This function has two real singularities at -1 and 1. Taylor polynomials approximate the function in an interval centered at the center of the series. Its radius is the distance to the nearest singularity.

Taylor polynomials (7): Rational function without real singularities

This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

Taylor polynomials: Rational function with two complex singularities

We will see how Taylor polynomials approximate the function inside its circle of convergence.

Complex Polynomial Functions(1): Powers with natural exponent

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

Complex Polynomial Functions(2): Polynomial of degree 2

A polynomial of degree 2 has two zeros or roots. In this representation you can see Cassini ovals and a lemniscate.

Complex Polynomial Functions(3): Polynomial of degree 3

A complex polinomial of degree 3 has three roots or zeros.

Complex Polynomial Functions(4): Polynomial of degree n

Every complex polynomial of degree n has n zeros or roots.

Polynomial functions and derivative (1): Linear functions

The derivative of a lineal function is a constant function.

Polynomial functions and derivative (2): Quadratic functions

The derivative of a quadratic function is a linear function, it is to say, a straight line.

Polynomial functions and derivative (3): Cubic functions

The derivative of a cubic function is a quadratic function, a parabola.

Definite integral

The integral concept is associate to the concept of area. We began considering the area limited by the graph of a function and the x-axis between two vertical lines.