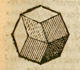
Article in 'Convergence: Where Mathematics, History, and Teaching Interact', the online journal of the Mathematical Association of America. Exploration of Kepler's discovery of the Rhombic Dodecahedron in its historical context.
Its name is Trapezo-rhombic dodecahedron.
Starting from what we know about the Rhombic Dodecahedron we are going to see three different approaches to this polyhedron.
1) Kepler discovered the Rhombic Dodecahedron looking at the bottom of bee cells. The Rhombic Dodecahedron has six rhombi in a belt.
We can imagine these six rhombi on the six faces of a bee cell. One 'end' of this belt is closed with three rhombi and the other with three
other rhombi.
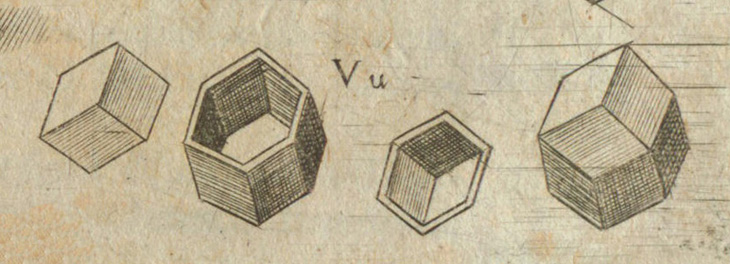
As the following video shows, you can cut in half one Rhombic Dodahedron and rotate 60º one part:
Then the Trapezo-rhombic dodecahedron has 6 faces that are rhombi and 6 trapezoidal faces.
This polyhedron has the same area and volume as the original Rhombic dodecahedron and also tessellate space.
2) A second approach is think the Rhombic dodecahedron as the result of squeezing cannonballs.
Kepler understood that the Rhombic Dodecahedron is related with the optimal sphere packing. If a precise structure of balls is squeezed we get rhombic dodecahedra.
If we play with clay balls we will easily notice that there ir two ways to put twelve balls around a central one.
With one of these two ways, compressing the balls we will get a Rhombic dodecahedron:
The second way is slightly different. If we squeeze this configuration we will get a Trapezo-rhombic dodecahedron.
3) We already know that there is a deep relation between the Rhombic dodecahedron and the cuboctahedron.
We can start with a cuboctahedron.
Cut it in half through one of its hexagonal sections:
And then rotate 60º one of these halves:
This new polyhedron is a polyhedron from Jonhson's family.
His name is Triangular orthobicupola (or twisted cuboctahedron).
Notice that the centers of the balls in our 'second configuration' are vertices of this polyhedron.
This two ways to pack balls are optimal. Their names are cubic close packing (or face-centered cubic packing) and
hexagonal close packing.
REFERENCES
Johannes Kepler, 'The Six Cornered Snowflake: a New Year's gif' - Paul Dry Books, Philadelphia, Pennsylvania, 2010. English translation of Kepler's book 'De Nive Sexangula'.
With notes by Owen Gingerich and Guillermo Bleichmar and illustrations by the spanish mathematician Capi Corrales Rodrigáñez.
D'Arcy Thompson, 'On Growth And Form' - Cambridge University Press, 1942.
Hugo Steinhaus, 'Mathematical Snapshots' - Oxford University Press - Third Edition.
Magnus Wenninger, 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell, 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter, 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Kepler understood that the Rhombic Dodecahedron is related with the optimal sphere packing. If a precise structure of balls is squeezed we get rhombic dodecahedra.
Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.
The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.
Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.
Tetraxis is a wonderful puzzle designed by Jane and John Kostick. We study some properties of this puzzle and its relations with the rhombic dodecahedron. We can build this puzzle using cardboard and magnets or using a 3D printer.
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.
NEXT
PREVIOUS
