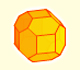
Density of the optimal sphere packing
When Kepler tried to answer the technical question of how to pack cannonballs in a ship he thought that the traditional way to pack oranges in a grocers stall was optimal.
That was known as Kepler Conjecture. It was very difficult to prove. At the end of the 20th century, Thomas Hales found a prove with the help of computers.

Kepler understood that the Rhombic Dodecahedron is related with the optimal sphere packing. If a precise structure of balls is squeezed we get rhombic dodecahedra.
What is not so difficult to calculate is the density of the optimal packing of spheres. In fact, it will be very easy if we use some basic properties of the Rhombic Dodecahedron.
To calculate this density of packing we usually consider a 'unit cell', a polyhedron that tessellate space. Typically we use prims, in particular, cubes.
Inside this unit cell there will be some spheres or sphere parts. We must calculate the ratio between the volume of the part occupied by spheres and the volume of our unit cell.
Sometimes it is not easy to visualize which sphere parts are inside the unit cell.
With our knowledge about the Rhombic Dodecahedron this task could not be much easier.
Two reasons:
Firstly, we can consider a Rhombic Dodecahedron as our unit cell. And inside this well known polyhedron there is only one ball.
Secondly, it is easy to calculate the volume of the unit cell and the volume of the sphere.
To show this situation I played with a semi transparent polyhedron and I put one red ball inside:



To calculate the volume of our Rhombic Dodecahedron we only needd to know that its volume is double the volume of the inscribed cube.
We can suppose that the inscribed cube has edge length equal 2. Then:
The volume of our unit cell is double the volume of the cube. We call this volume D.
Very easily we have found the volume of the unit cell.
Now, the volume of the sphere. Playing with a model we can realize that this inscribed sphere touches the edges of the inscribed cube, it is the midsphere of the cube.
We can calculate the radius of this sphere:
We call S the volume of the sphere :
Then, the density of the optimal sphere packing is:
Very easy calculation.
REFERENCES
Johannes Kepler, 'The Six Cornered Snowflake: a New Year's gif' - Paul Dry Books, Philadelphia, Pennsylvania, 2010. English translation of Kepler's book 'De Nive Sexangula'.
With notes by Owen Gingerich and Guillermo Bleichmar and illustrations by the spanish mathematician Capi Corrales Rodrigáņez.
D'Arcy Thompson, 'On Growth And Form' - Cambridge University Press, 1942.
Hugo Steinhaus, 'Mathematical Snapshots' - Oxford University Press - Third Edition.
Magnus Wenninger, 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell, 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter, 'Matematical Recreations & Essays', The MacMillan Company, 1947.
MORE LINKS

Humankind has always been fascinated by how bees build their honeycombs. Kepler related honeycombs with a polyhedron called Rhombic Dodecahedron.

Kepler understood that the Rhombic Dodecahedron is related with the optimal sphere packing. If a precise structure of balls is squeezed we get rhombic dodecahedra.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.

We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.

Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.

You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.

A chain of six pyramids can be turned inwards to form a cube or turned outwards, placed over another cube to form the rhombic dodecahedron.

The obtuse angle of a rhombic face of a Rhombic Dodecahedron is known as Maraldi angle. We need only basic trigonometry to calculate it.

There are two essential different ways to pack spheres in an optimal disposition. One is related with the Rhombic Dodecaedron and the other to a polyhedron called Trapezo-rombic dodecahedron..

Tetraxis is a wonderful puzzle designed by Jane and John Kostick. We study some properties of this puzzle and its relations with the rhombic dodecahedron. We can build this puzzle using cardboard and magnets or using a 3D printer.
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.













 PREVIOUS
PREVIOUS