Kepler, cannonballs and the Rhombic Dodecahedron
Kepler understood the relation between the Rhombic Dodecahedron and the bottom of bee cells. But he thought about this polyhedron from different points of view.
Each of these approaches gives us a complementary vision of this polyhedron.
Kepler linked his observation of how the seeds of the pomegranate grows with a technical problem: what is the optimal way to stack cannonballs in a ship.
The origin of this question seem to be a letter sent to Kepler for the english astronomer and mathematician Thomas Harriot. Harriot was a friend and adviser of Sir Walter Raleigh and the question try to answer a practical question.
This question led Kepler to study the optimal packing of spheres and his proposed solution is what now call as 'Kepler conjecture'.
This is a complex question and here we only want to see the relation between the packing of spheres and the Rhombic Dodecahedron.
Basically we can say that Kepler thought that we get the optimal packing of spheres if we surround a cannonball with six balls in one layer. Then he put three balls above and another three below. In total, twelve balls are surrounding a ball in the center.
Then, Kepler imagination and creativity come into play. He said that if we compress this structure of cannonballs, the central ball will deform into a rhombic dodecahedron. And if we had a lot of balls organized in layers in the same way after compression we will get a big amount of rhombic dodecahedra.
That experiment deserve a tray. The result is spectacular and incredible simple.
To star the experiment I prepared thirteen clay balls.

In the first layer I put a center ball surrounded by six others in an hexagonal pattern. In the holes I put three more above and three below.


The result is this structure:

What we are doing has a lot to do with the way that Kepler discovered the Rhombic Dodecahedron looking at the bottom of bee cells.
At the bottom of the bee cell Kepler noticed that there were three rhombi. We can think that these three rhombi correspond with the three balls below.
Six balls in the middle correspond with six rhombi that we can put on the six faces of the hexagonal cell.
Our polyhedron is closed with three more rhombi. These are the three last balls above.
To sum up, we have twelve balls surroundig a central ball.
We want to squeeze this structure. To avoid sticking I put oil with a brush.

I squeezed carefully:


Withoug effort a ball with twelve rhombic shapes has formed:

We open it and we can see the result: a central ball has been deformed into a Rhombic Dodecahedron.


Our Rhombic Dodecahedron is quite perfect.
A very simple and effective experiment to show that, once again, that Kepler was right.

D'Arcy Thompson wrote about this experiment and the relation with honeybees:
If we experiment, not with cylinders but with spheres, if for instance we pile bread-pills together and then submit the whole to a uniform preassure, as we shall presently find that Buffon did: each ball (like the seeds of pomegranate, as Kepler said) will be in contact with twelve others, six in one plane, three below and three above, and under compression it will develop twelve plane surfaces. It will repeat, above and below, the conditions to which the bee's cell is subject at one end only; and, since the sphere is symmetrically situated towards its neighbours on all sides, it follows that the twelve planes sides to which its surface has been reduced will be all similar, equal and similarly situated. Moreover, since we have produced this result by squeezing our original spheres close togheter, it is evident that the bodies so formed completely fill space. The regular solid which fulfils all these conditions is the rhombic dodecahedron. The bee's cell is this figure incompletely formed; it represents, so to speak, one-half of that figure, with its apex and the six adjacent corners proper to the rhombic dodecahedron, but six sides continued, as a hexagonal prism, to an open or unfinished end.
If we take a closer look to this ball structure we will notice that centers of these twelve balls are vertices of an archimedean polyhedron called cuboctahedron.

The same construction made with plastic balls:

There is a deep relationship between the cuboctahedron and the Rhombic Dodecahedron. For now I am going to highlight only two properties that we can notice playing with this structure.
It is highly recommended to build a real model of a cuboctahedron.
The twelve vertices of the cuboctahedron and its twenty four edges are in four hexagonal sections of this polyhedron. They correspond with four belts of six rhombi that the Rhombic Dodecahedron has.
A model of a cuboctahedron made of cardboard (with magnets inside). We can see one of the four hexagonal sections.


The distance between two balls is always the same. Then, the distance between each of the vertices of the cuboctahedron and its center is equal to the length of one edge.

REFERENCES
Johannes Kepler, 'The Six Cornered Snowflake: a New Year's gif' - Paul Dry Books, Philadelphia, Pennsylvania, 2010. English translation of Kepler's book 'De Nive Sexangula'.
With notes by Owen Gingerich and Guillermo Bleichmar and illustrations by the spanish mathematician Capi Corrales Rodrigáñez.
D'Arcy Thompson, 'On Growth And Form' - Cambridge University Press, 1942.
Hugo Steinhaus, 'Mathematical Snapshots' - Oxford University Press - Third Edition.
Magnus Wenninger, 'Polyhedron Models', Cambridge University Press.
Peter R. Cromwell, 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', (Section 4.7. Sphere-Packs, pp. 195-197), Oxford University Press, Second Edition, 1961.
W.W. Rouse Ball and H.S.M. Coxeter, 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Martin Gardner, 'New Mathematical Diversions', Chapter 7: Packing Spheres, The Mathematical Association of America, 1995.
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.

We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.

Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.

You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.

A chain of six pyramids can be turned inwards to form a cube or turned outwards, placed over another cube to form the rhombic dodecahedron.

The obtuse angle of a rhombic face of a Rhombic Dodecahedron is known as Maraldi angle. We need only basic trigonometry to calculate it.

There are two essential different ways to pack spheres in an optimal disposition. One is related with the Rhombic Dodecaedron and the other to a polyhedron called Trapezo-rombic dodecahedron..

Using a basic knowledge about the Rhombic Dodecahedron, it is easy to calculate the density of the optimal packing of spheres.
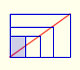
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.

Tetraxis is a wonderful puzzle designed by Jane and John Kostick. We study some properties of this puzzle and its relations with the rhombic dodecahedron. We can build this puzzle using cardboard and magnets or using a 3D printer.

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.