The rhombicuboctahedron is an Archimedean polyhedron. Its faces consist of 8 triangles and 12+6 squares.
The polyhedron that we are going to study in this page is very similar to the
rhombicuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the rhombicuboctahedron.
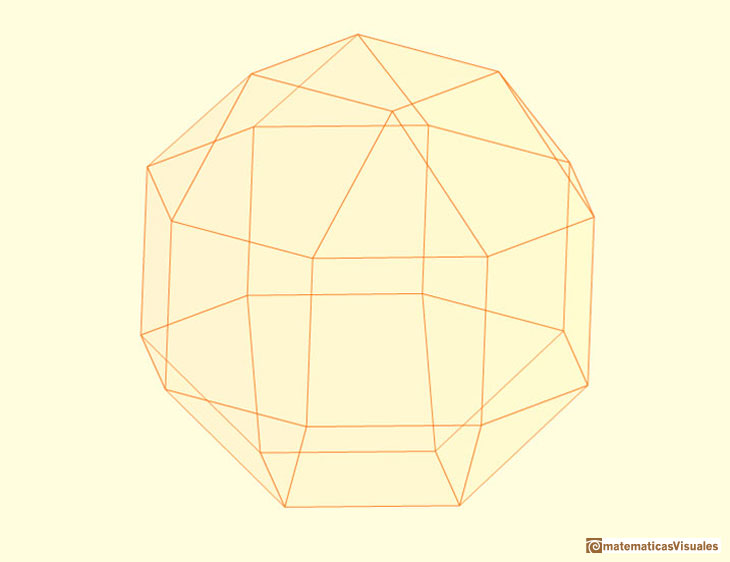
"In attempting to make a model of his polyhedron, J.C.P. Miller
accidentally discovered a 'pseudo-rhombicuboctahedron', bounded
likewise by 8 triangles and 18 squares, and isogonal in the loose or
'local' sense (each vertex being surrounded by one triangle and
three squares), but not in the strict sense (which implies that
the apearance of the solid as a whole must remain the same when
viewed from the direction of each vertex in turn)."
(Ball and Coxeter, p. 137)
This polyhedron is one of the Johnson solids. It has been rediscovered many times.
"It has been called by a variety of names:
the pseudo rhomb-cub-octahedron, Miller's solid, and elongated square gyro
bicupola. The last of these names is Johnson's and it indicates how the
solid is constructed from elementary polyhedra: take two square cupolas
(square bicupola) rotated relative to one another (gyro) and separate by a
prism (elongated)." (Cromwell, p.89)
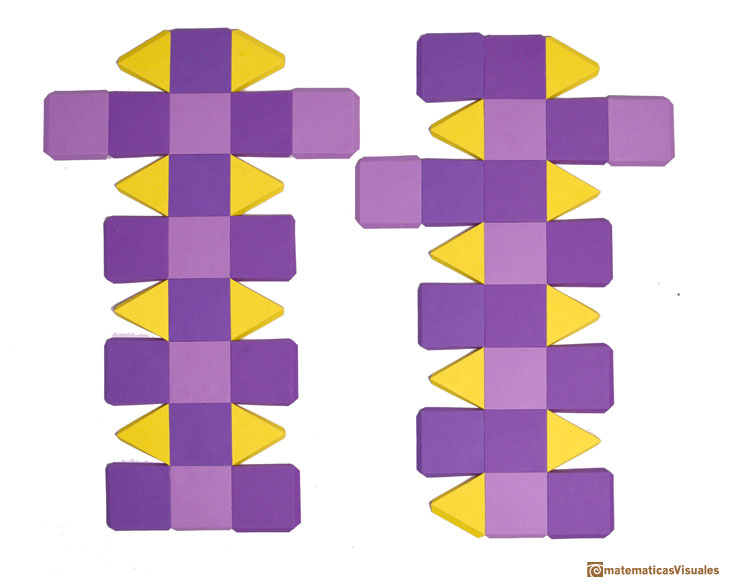
These two polyhedra have the same faces but they cannot be made from the same net.
It is easy to build a pseudo rhombicuboctahedron with cardboard. The rhombicuboctahedron is on the left and the pseudo rhombicuboctahedron is on the
right.

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!
REFERENCES
W.W.W. Rouse Ball and H.S.M. Coxeter, 'Mathematical Recreatins & Essays', The Macmillan Company, New York, 1947.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999. (pp. 89 and 366-369)
MORE LINKS

We can see the interior of the augmented rhombicuboctahedron. Luca Pacioli wrote that you 'can see the interior only with your imagination'.

Starting with a Rhombicubotahedron we can add pyramids over each face. The we get a beautiful polyhedron that it is like a star.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the dodecahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the Campanus' sphere.

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!

A very simple technique to build complex and colorful polyhedra.

Material for a session about polyhedra (Zaragoza, 7th November 2014). We study the octahedron and the tetrahedron and their volumes. The truncated octahedron helps us to this task. We build a cubic box with cardboard and an origami tetrahedron.

Material for a session about polyhedra (Zaragoza, 23rd Octuber 2015) . Building a cube with cardboard and an origami octahedron.

Material for a session about polyhedra (Zaragoza, 13th Abril 2012).

Material for a session about polyhedra (Zaragoza, 9th May 2014). Simple techniques to build polyhedra like the tetrahedron, octahedron, the cuboctahedron and the rhombic dodecahedron. We can build a box that is a rhombic dodecahedron.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.
The truncated tetrahedron is an Archimedean solid made by 4 triangles and 4 hexagons.
When you truncate a cube you get a truncated cube and a cuboctahedron. If you truncate an octahedron you get a truncated octahedron and a cuboctahedron.













 NEXT
NEXT
 PREVIOUS
PREVIOUS
































