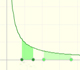
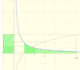
"Mostración" de una propiedad de la integral de la hipérbola

Para justificar la propiedad de la hipérbola

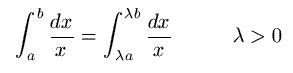
podemos dividir el intervalo entre a y b y considerar varios rectángulos que aproximan el área. Si los extremos del intervalo los multiplicamos por un número positivo se puede dividir ese nuevo intervalo en el mismo número de rectángulos. Cada uno de esos rectángulos tiene la misma área que los correspondientes en el primer intervalo.

En el applet podemos modificar los extremos de los intervalos y también el número de rectángulos de la partición.

Pulsando la animación, los rectángulos se transforman de modo continuo.

El logaritmo natural se puede definir como una integral de la hipérbola y, usando esta propiedad, podemos justificar que el logaritmo de un producto es la suma de los logaritmos.

REFERENCIAS

Markushevich - Áreas y logaritmos. Ed. Mir.

ENLACES

Exponenciales y Logaritmos (3): Una propiedad de la integral de la hipérbola

Hemos definido la función logaritmo como una integral de la hipérbola equilátera. Esta integral tiene una importante propiedad que nos permitirá usar los logaritmos para transformar multiplicaciones en sumas.

Exponenciales y Logaritmos (4): El logaritmo de un producto

Usando los logaritmos podemos multiplicar dos números haciendo una suma: el logaritmo de un producto es igual a la suma de los logaritmos de los factores.