When modeling a situation where there are n independent trials with a constant probability p of "success" in each test we use a binomial distribution.
For example, if we toss n equal coins and we count heads as success, the probability of getting head can be any value between 0 and 1.
A binomial distribution is characterized by two parameters: n (a natural number) and p a number between 0 and 1.
If a random variable X follows the binomial distribution with parameters n and p, we write
The probability of getting exactly k successes in n trials is given by the probability mass function (or probability density function):
where
The later expression is known as the binomial coefficient, "n choose k", or the number of possible ways to choose k successes from n observations. The binomial coefficients form the rows of Pascal's triangle and can be calculated using factorials:
When p = 0.5 the probability mass function is symmetric:
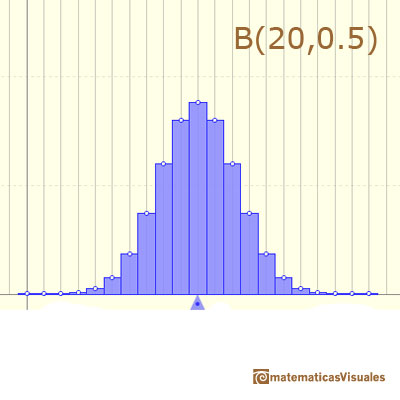
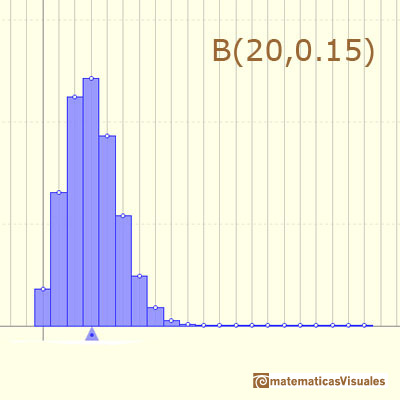
In other cases the function is asymmetric:
Mean and Variance of the Binomial Distribution are:
In the applet we can change the parameter n.
The mean is represented by a triangle and it can be seen as a point of equilibrium. By dragging we can modify parameter p.
The gray points control vertical and horizontal scales. Pressing the right button and dragging you can move left and right.
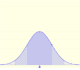
We can show a normal curve that has the same mean and variance as the binomial distribution.
In some cases, this normal curve is close to the binomial and can be used for calculations.
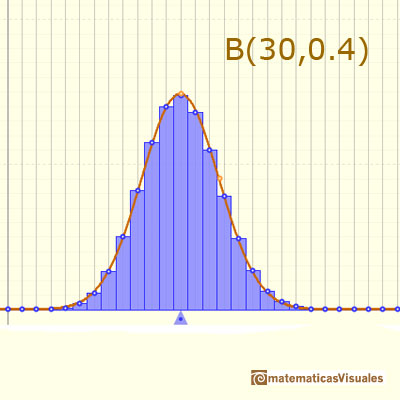
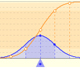
You can see why it is recommended to extend the interval for which you want to calculate the probability of the binomial in 0.5 above and below to use the normal distribution to approximate the probability (correction for continuity adjustement).
For example:
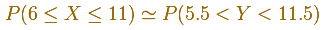
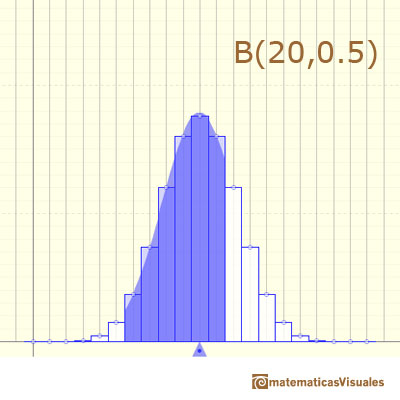
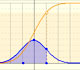
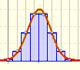
In other cases, this normal curve is not a good approximation to the binomial distribution:
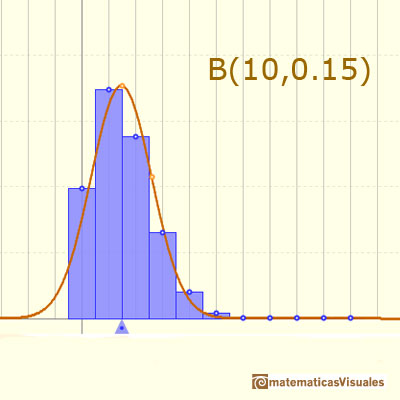
Even with the correction for continuity adjustement the approximation is not accurate:
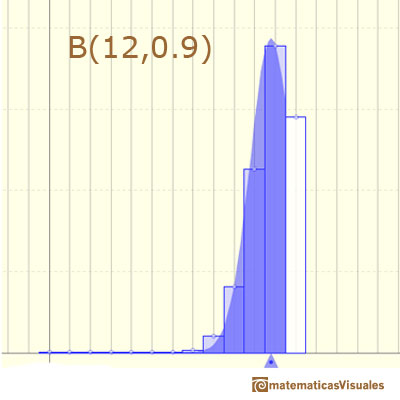
You can see more about the Normal approximation to the Binomial.
LINKS
|
Normal approximation to Binomial distribution
In some cases, a Binomial distribution can be approximated by a Normal distribution with the same mean and variance.
|
|
Normal distribution
The Normal distribution was studied by Gauss. This is a continuous random variable (the variable can take any real value). The density function is shaped like a bell.
|
|
One, two and three standar deviations
One important property of normal distributions is that if we consider intervals centered on the mean and a certain extent proportional to the standard deviation, the probability of these intervals is constant regardless of the mean and standard deviation of the normal distribution considered.
|
|
Calculating probabilities in Normal distributions
It may be interesting to familiarize ourselves with the probabilities correspondig to different intervals in normal distributions.
|
|
Poisson distribution
Poisson distribution is discrete (like the binomial) because the values that can take the random variable are natural numbers, although in the Poisson distribution all the possible cases are theoretically infinite.
|
|
Student's t-distributions
Student's t-distributions were studied by William Gosset(1876-1937) when working with small samples.
|
|