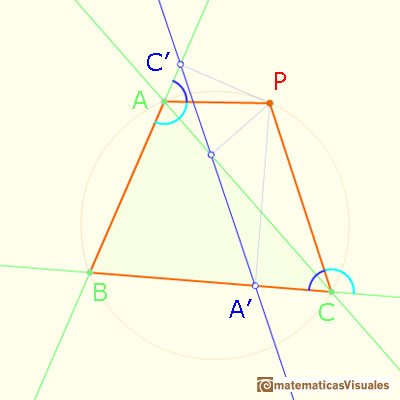
We can start with a triangle and its circunscribed circle.
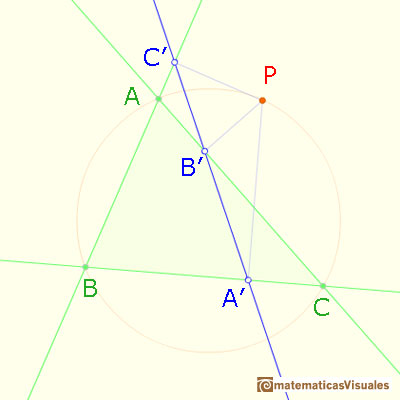
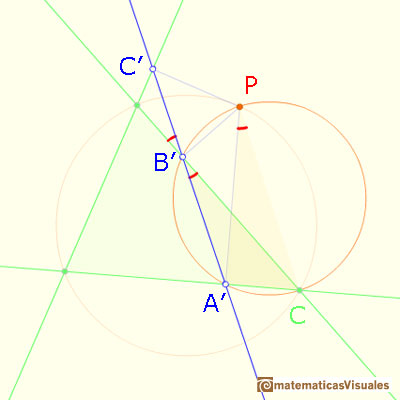
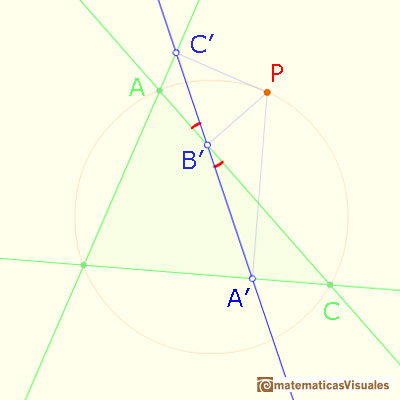
Given a point P on the circumcircle of a triangle,
the feet of the perpendiculars from P to the three sides all lie on a straight line (Simson line or Simson-Wallace line)
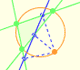
Each point in the circle circunscribed to a triangle give us a line (Wallace-Simson line)
We are going to see this property using this notation:
We have taken P to lie on the arc AC that does not contain B. Other cases can be derived by re-naming A, B, C.
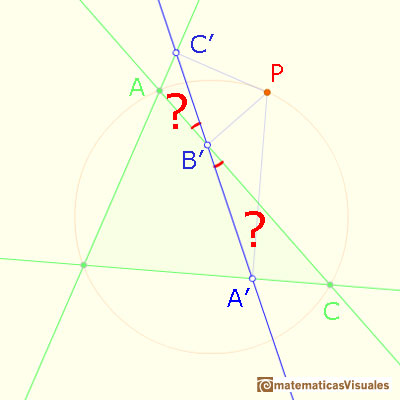
If we can prove that these two angles are equal then points A', B', C' will be collinear.
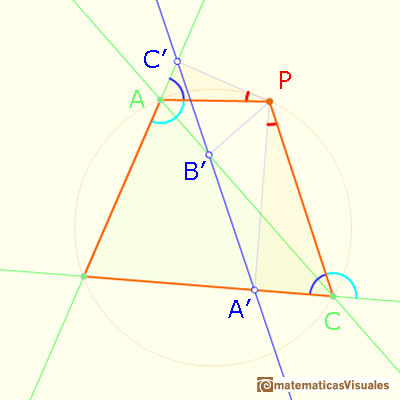
We can use a consequence of a circle property (Euclides, III.21 or III.22) that
saids that the opposite angles of every convex cuadrangle inscribed in a circle are together equal to two right angles.
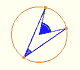
Central angle in a circle is twice the angle inscribed in the circle.
Two right triangles are similar, then:
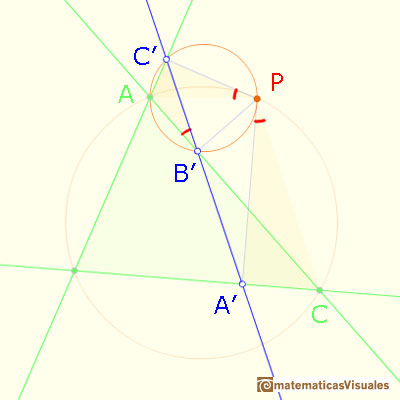
Points A, B', P, C' lies on a circle:
And points B',A',C,P lies on a circle:
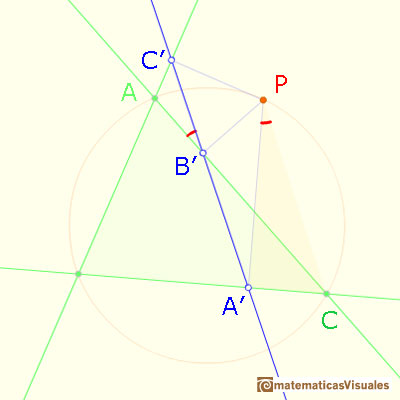
Then points A', B', C' are collinear. This is called Simson Line or Simson-Wallace Line of P.
REFERENCES
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: John Wiley and sons, 1969.
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.
MORE LINKS
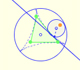
Steiner deltoid is a hypocycloid related with the nine point circle of a triangle.
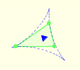
Steiner Deltoid and the Morley triangle are related.

Central angle in a circle is twice the angle inscribed in the circle.
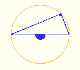
Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case I: When the arc is half a circle the inscribed angle is a right angle.

Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case II: When one chord that forms the inscribed angle is a diameter.
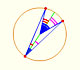
Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.
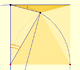
Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.
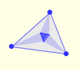
The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle (Morley's triangle)
Interactive animation about John Conway's beautiful proof of Morley's Theorem

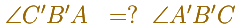
 NEXT
NEXT




















 PREVIOUS
PREVIOUS


