|
|
|
Morley's Theorem
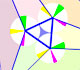
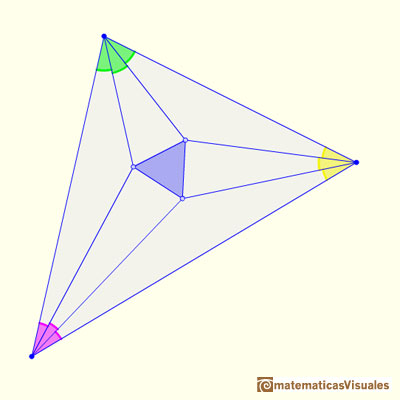
The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle called the Morley Triangle.
This was a surprising discovery made by Frank Morley (1899).
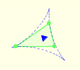
We start with any triangle and trisect each of its angles...
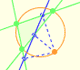
Extend the trisections ...
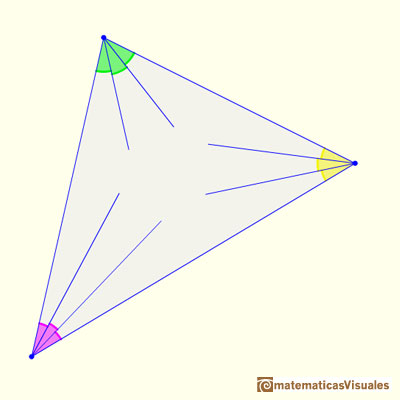
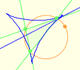
We consider the three points of intersection of the adjacent trisectors ...
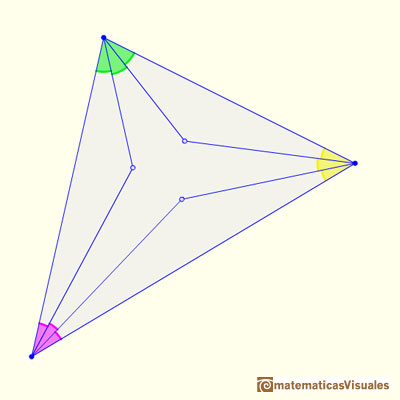
And we always get an equilateral triangle.
In the near future I am going to publish an animation with John Conway's proof of Morley's Theorem.
REFERENCES
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: John Wiley and sons, 1969.
NEXT
Interactive animation about John Conway's beautiful proof of Morley's Theorem
MORE LINKS
Each point in the circle circunscribed to a triangle give us a line (Wallace-Simson line)
Steiner deltoid is a hypocycloid related with the nine point circle of a triangle.
Central angle in a circle is twice the angle inscribed in the circle.