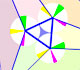
|
|
|
Steiner Deltoid and Morley triangle
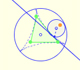
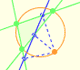
The three cuspidal points of the Steiner deltoid are the vertices of an equilateral triangle.
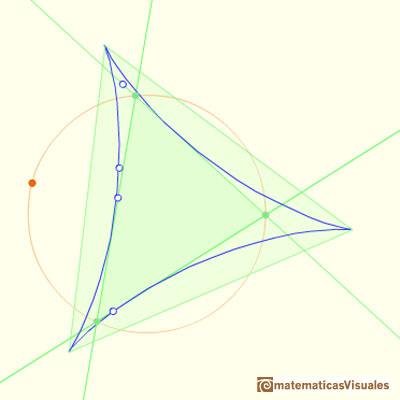
The sides of this equilateral triangle are parallel to those of the Morley triangle and its orientation is inverse.
REFERENCES
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.
de Guzmán, Miguel 'The envelope of the Wallace-Simson lines of a triangle. A simple proof of the Steiner theorem on the deltoid'.
RACSAM, vol. 95, 2001.
Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: John Wiley and sons, 1969.
PREVIOUS
Steiner deltoid is a hypocycloid related with the nine point circle of a triangle.
MORE LINKS
Each point in the circle circunscribed to a triangle give us a line (Wallace-Simson line)
Central angle in a circle is twice the angle inscribed in the circle.
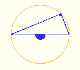
Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case I: When the arc is half a circle the inscribed angle is a right angle.
Interactive 'Mostation' of the property of central and inscribed angles in a circle. Case II: When one chord that forms the inscribed angle is a diameter.
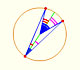
Interactive 'Mostation' of the property of central and inscribed angles in a circle. The general case is proved.
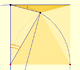
Using a ruler and a compass we can draw fifteen degrees angles. These are basic examples of the central and inscribed in a circle angles property.
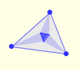
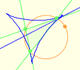
The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle (Morley's triangle)
Interactive animation about John Conway's beautiful proof of Morley's Theorem