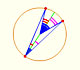
CASO 1. Si un ángulo inscrito subtiende un diámetro entonces es un ángulo recto.

Este es un caso particular del Teorema del ángulo central pues en este caso el ángulo central es un ángulo llano, de 180º.

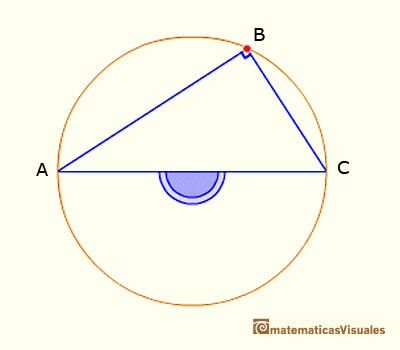
Queremos probar que

La base de estos resultados es "pons asinorum", es decir, que los ángulos de la base de un triángulo isósceles son iguales.

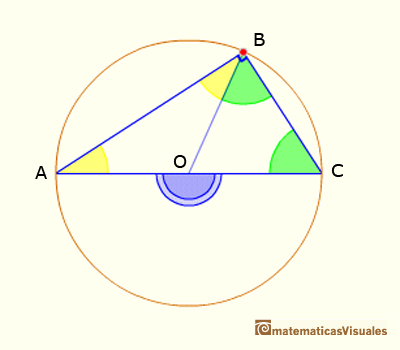
Sumando los ángulos del triángulo ABC podemos escribir_

Dividiendo por dos:

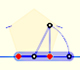
Esto termina la demostración del Caso I. El siguiente caso es cuando una de las cuerdas que forman el ángulo inscrito es un diámetro. Podemos ver una demostración interactiva de la propiedad de los Ángulos central e inscrito en una circunferencia |Caso II.

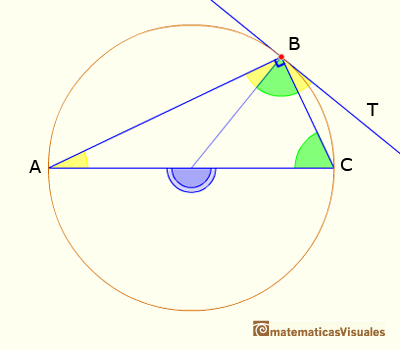
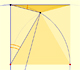
Ahora podemos probar un caso particular de la Proposición III.32 de los Elementos de Euclies (sobre el ángulo entre una tangente y una secante):

MÁS ENLACES

Ángulos central e inscrito en una circunferencia | Demostración | Caso General

Demostración interactiva de la propiedad de los ángulos central e inscrito en una circunferencia. Prueba del caso general.

Dibujando ángulos de quince grados con regla y compás

Usando regla y compás podemos dibujar ángulos de 15 grados. Son ejemplos básicos de las propiedades de los ángulos central e inscrito en una circunferencia.

Dibujo de un pentágono regular con regla y compás

Podemos dibujar un pentágono regular dado uno de sus lados construyendo la razón áurea con regla y compás.

Aproximación de Durero de un pentágono regular

En su libro 'Underweysung der Messung' Durero dibujó un pentágono no regular con regla y compás con apertura fija. Es una construcción simple y una muy buena aproximación de un pentágono regular.

La diagonal de un pentágono regular y la razón áurea

La diagonal y el lado de un pentágono regular están en proporción áurea. El punto de intersección de dos diagonales de un pentágono regular divide a ambas en la razón áurea o 'en razón extrema y media'.