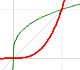
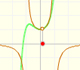
A rational function is a function that can be written as the quotient of two polynomials.
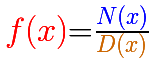
If the denominator is a number (a polynomial of degree 0) then the function is a polynomial. Then polynomial functions are rational functions. But, in these pages we are going to consider only rational functions that in the denominator have a polynomial of degree greater than 0.
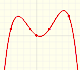
These functions are richer than polynomial functions.
We are going to learn:
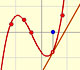
- Singularities: In some cases, some values of x are problematic. An special role is played by those values of x with which the denominator becomes zero. You can not divide by zero and you can not calculate the value of the function in those points, the function is not defined.
We say that these points do not belong to the domain of the function. The domain of a rational function is determined by the restriction imposed by the denominator: dividing by 0 is impossible.
The domain is the set of real numbers for which the function is defined. In the case of rational functions, it is the set of all real numbers which are not zeros of the denominator. To find the domain of a real function, we must then look for the real zeros of its denominator.
Those points are called singularities and it is interesting to see how the function behaves near these points.
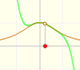
- x-intercepts: The x-intercepts are values of x where the graph crosses the x-axis. It is to say are the values of x for which f(x) = 0.
- Continuity: rational functions are continuous in its domain.
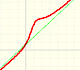
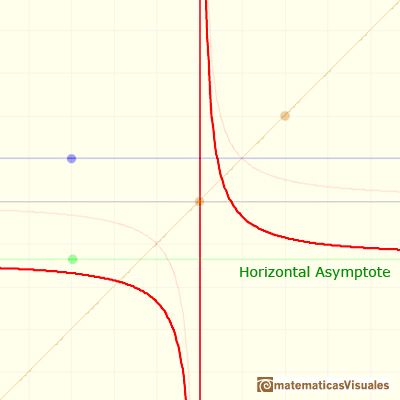
- End Behavior: It is interesting to study the function behavior when x become larger and larger in absolute value (it is to say, positive or negative). We are going to see that in some cases the function approaches a straight line (horizontal or oblique). Then we say that the function has an horizontal asymptote or a oblique (or slant) asymptote. In all cases end behavior is determined by a polynomial function.
We start our study with Linear rational functions. A Linear rational function is a rational function with a numerator that is a number or a polynomial of degree 1 and the denominator is a polynomial of degree 1.
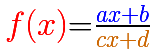
The simplest rational function is
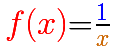
This curve is called a hyperbola.
When x = 0, you can not calculate the value of the function because you can not divide by zero (sometimes we say that 'the quotient becomes infinite'). The function is not defined at x = 0. Then, the domain of this function is:
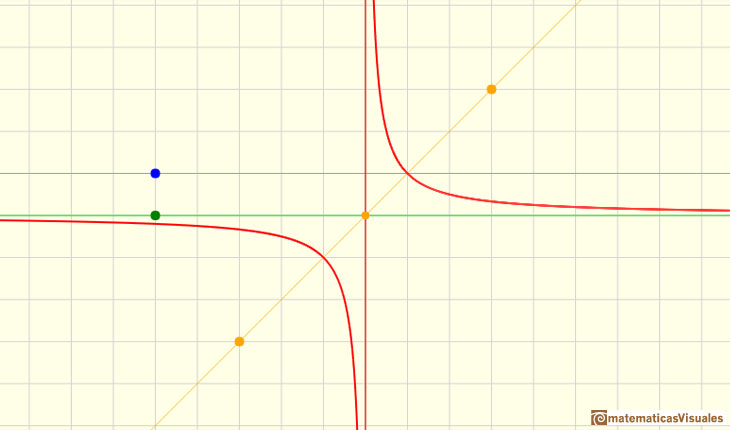
For x = 1 we have y = 1. For x > 1 the numerator is smaller than the denominator and the quotient is less than 1.
Let us find how the function behaves if x increases in absolute value. As x increases the fraction 1/x decreases. "Therefore in moving from zero to the right, the curve y=1/x drops lower and lower, and it can approach the x-axis to within an arbitrarily small distance." When you consider x bigger and bigger then the quotient approaches zero and the function behaves like a horizontal line. We call it an horizontal asymptote.
The line y=b is a horizontal asymptote for the graph of f(x) if f(x) approach b as x increases or decreases without bound.
In this case, the horizontal asymptote is the x-axis:
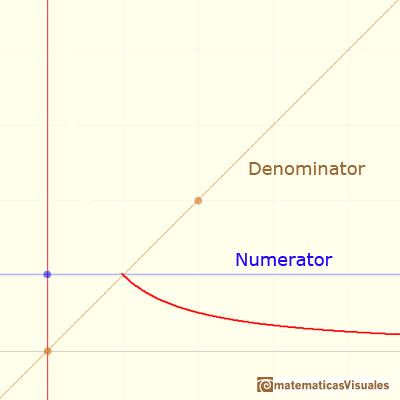
When x approaches 0 from the side of 1 (positive values), the denominator approaches 0 while the numerator remains equal to 1. y becomes as large as we please. Therefore the quotient increases without limit and we obtain the branch going off to infinity.
If x approaches zero from the left (negative values) then the graph of the function moves down.
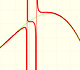
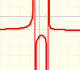
We say that the function has a vertical asymptote. The graph is separated into two branches.
The line x=a is a vertical asymptote for the graph of f(x) if f(x) either increases or decreases without bound as x approaches a from the right or from the left.
A rational function will have a vertical asymptote at the zeros of the denominator (as long as they are not zeros of the numerator)
In this case the vertical asymptote is:
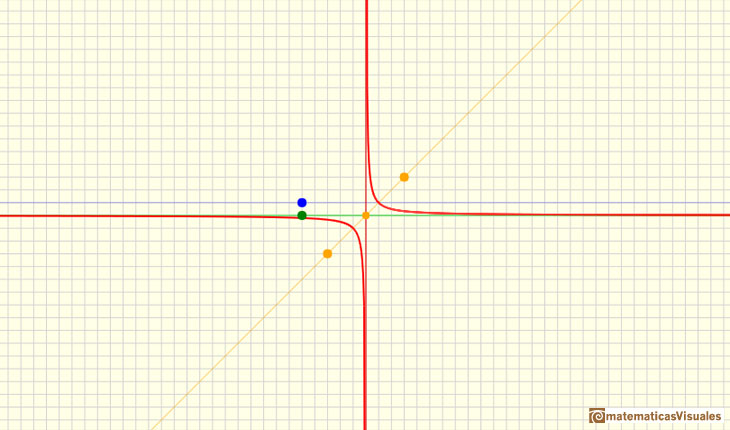
If we add a number to the denominator the result is a translation of the hyperbola along the x-axis:
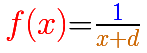
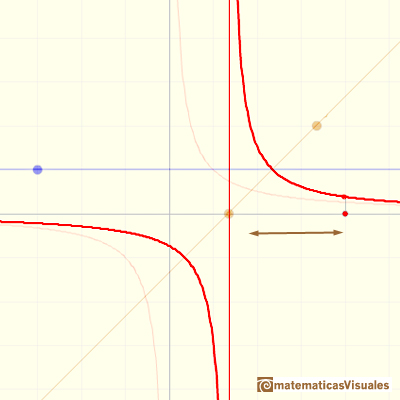
If we change the slope of the straight line in the denominator the result is a contraction or expansion along the y-axis:
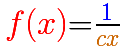
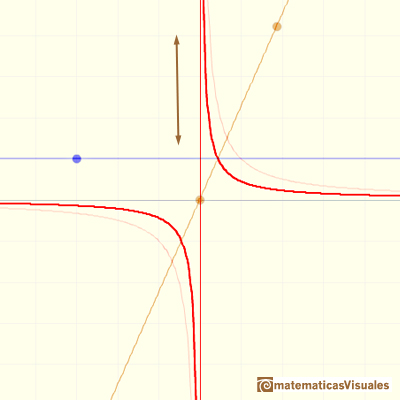
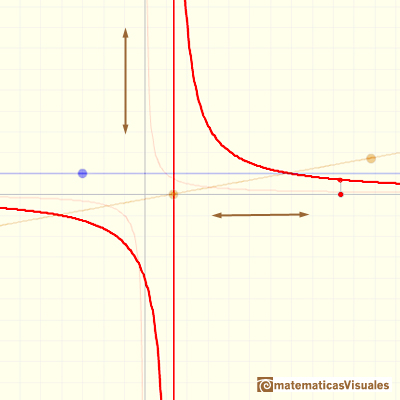
Both, translation and contraction:
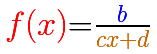
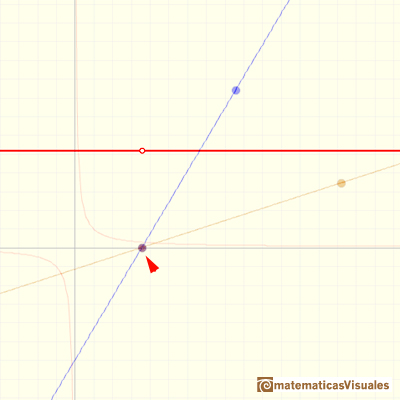
Now we are going to consider more general Linear rational functions in which both the numerator and the denominator are polynomial of degree 1, straight lines (we consider c not equal to 0).
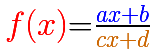
The domain of a linear rational function is:
A linear rational function has one horizontal asymptote:
If numerator and denominator has not a common factor, then the rational function has one vertical asymptote:
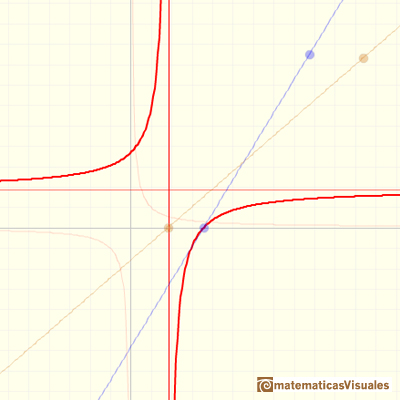
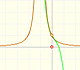
When both lines have the same root (numerator and denominator have a common factor) we have a "hole", an avoidable or removable singularity. In these cases, sometimes we talk about 'removable' or 'avoidable' discontinuity (although usually we define continuity only for values in the function's domain, then we can consider talking about discontinuity in this context as an abuse of terminology). The idea is that we can simplify the fraction and then we get a new function almost equal than the original one but with a bigger domain (filling the gap).
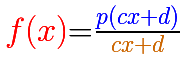
Removable singularities are singularities for which it is possible to assign a value in such a way that the function becomes continuous.
Rational functions can have two kinds of singularities: In some cases there it is a vertical asymptote (non-removable singularity or essential) and in other cases there is a 'hole' (removable singularity).
It is interesting to differentiate two kinds of rational functions: proper and improper rational functions. A proper rational function is one in which the degree of the numerator is less than the degree of the denominator. Otherwise it is called improper. For example, the function 1/x is proper but, in general, linear rational functions are improper because both numerator and denominator have degree 1.
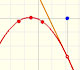
If a rational function is improper you can divide the numerator by the denominator and then you can write the rational function as the sum of a polynomial and a proper rational function:
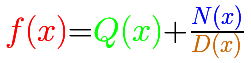
The polynomial controls the behavior of the function when x is big in absolute value. This is because a proper rational function contributes very little to the values of the function for large |x|.
With Linear rational functions, when you divide you get a quotient that is a number:
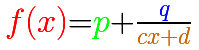
In the mathlet you can play with these three elements of a Linear rational function: a number (p, in green, a horizontal line), another number in the numerator of the proper rational function (q, in blue, a horizontal line) and a straight line in the denominator
You can see how the number p controls the end behavior of the rational function.
Any Linear fractional function "can be written in an analogous way, separating its 'integral part'. Consequently, the graphs of all linear fractional functions [not degenerate] are hyperbolas (translated differente distances along the coordinate axes and stretched in different ratios along the y-axis)". ["Functions and Graphs", pag. 64]
In this case, the horizontal asymptote is:
For example:
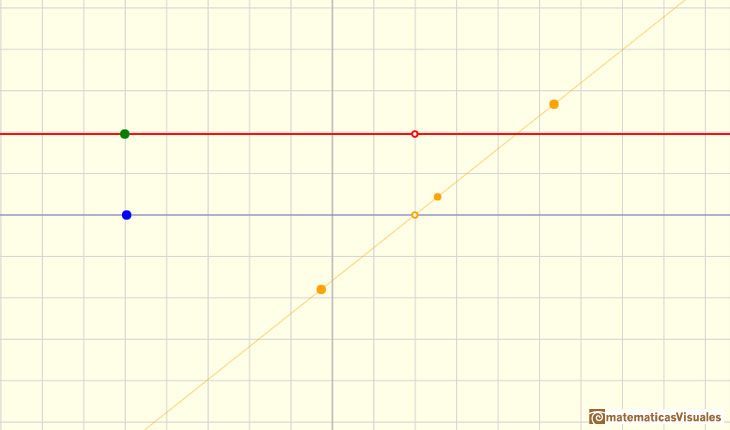
You can write the degenerate case (with a hole):
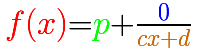
REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS