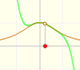
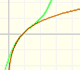
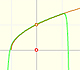
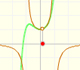
The rational function

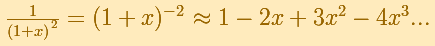
is, as in the example of the square root or in the rational function 1, a special case of Newton's Binomial Theorem. We can calculate its Taylor's series at x = 0 easily.

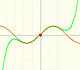
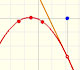
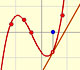
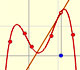
This function has a singularity at the point x =- 1. The approximation is good in ranges from -1 to +1. Again we find a useful approach that is centered on the origin.

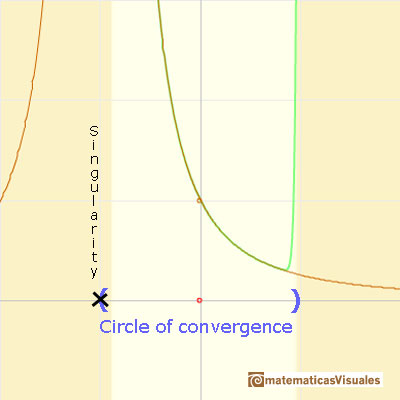
At the point x = +1 the ordinates increase indefinitely with the order, and alternate in sign.

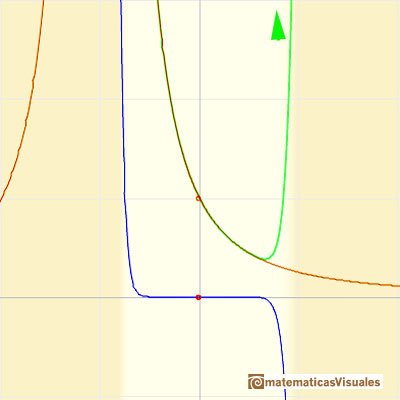
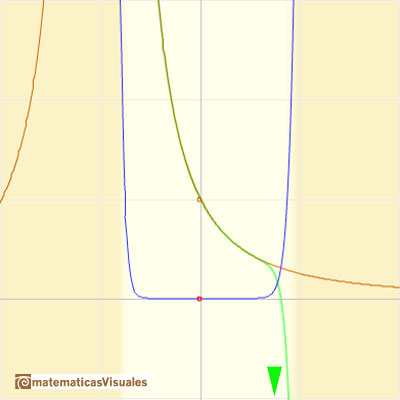
We can compare this behavior with that of the rational function 1.

Klein wrote: "The theoretical consideration of Taylor's series cannot be made complete without going over to the complex variable. It is only then that one can understand the sudden ceasing of the power series to converge at places where the function is entirely regular. To be sure, one might be satisfied, in the case of our examples, by saying that the series cannot converge any farther to the right than to the left, and that the convergence must cease at the left because of the singularity at x = -1." (Klein, p. 227)

We can see more examples to understand better this question, for example in Taylor polynomials (6): Rational function with two real singularities.

REFERENCES

MORE LINKS

Taylor polynomials (7): Rational function without real singularities

This is a continuos function and has no real singularities. However, the Taylor series approximates the function only in an interval. To understand this behavior we should consider a complex function.

Mercator and Euler: Logarithm Function

Mercator published his famous series for the Logarithm Function in 1668. Euler discovered a practical series to calculate.

Taylor polynomials: Rational function with two complex singularities

We will see how Taylor polynomials approximate the function inside its circle of convergence.

Taylor polynomials (1): Exponential function

By increasing the degree, Taylor polynomial approximates the exponential function more and more.

Taylor polynomials (2): Sine function

By increasing the degree, Taylor polynomial approximates the sine function more and more.

Taylor polynomials (3): Square root

The function is not defined for values less than -1. Taylor polynomials about the origin approximates the function between -1 and 1.

Polynomial functions and derivative (1): Linear functions

The derivative of a lineal function is a constant function.

Polynomial functions and derivative (2): Quadratic functions

The derivative of a quadratic function is a linear function, it is to say, a straight line.

Polynomial functions and derivative (3): Cubic functions

The derivative of a cubic function is a quadratic function, a parabola.

Polynomial functions and derivative (4): Lagrange polynomials (General polynomial functions)

Lagrange polynomials are polynomials that pases through n given points. We use Lagrange polynomials to explore a general polynomial function and its derivative.