When we consider a cubic function in the complex plane it always have three roots.
They are particular cases of
polynomial functions.
The Fundamental Theorem of Algebra states that every polynomial function of degree n has exactly n complex zeros, not necessarily distinct.
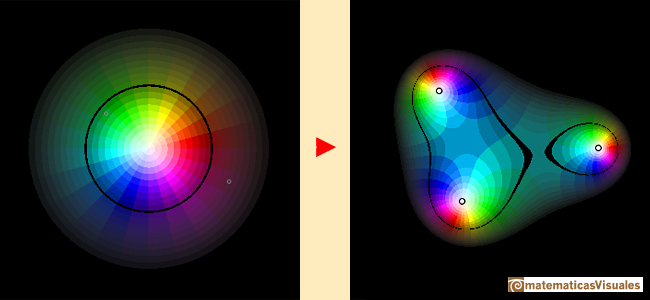
You start the applet seeing the representantion of the cubic polynomial function whose zeros are the cubic roots of unity.
When you change the roots (or zeros) the applet represents a more general cubic function
You can move the dots that represent the different zeros or roots (three simple roots) of the polynomial function.
If some of these roots are the same we say that they have double or triple multiplicity.
The multiplicity of the zero is represented by the number of times that the color cycle (red->green->blue) goes round the root.
This is another example with three simple roots:
In this example you can see a double root and a simple root:
Round the double root the color cycle repeat itself twice.
This is an example of a triple root:
Round the triple root the color cycle repeat itself three times.
You can see another video with darker colors:
MORE LINKS

Complex power functions with natural exponent have a zero (or root) of multiplicity n in the origin.

Every complex polynomial of degree n has n zeros or roots.
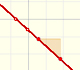
Two points determine a stright line. As a function we call it a linear function. We can see the slope of a line and how we can get the equation of a line through two points. We study also the x-intercept and the y-intercept of a linear equation.
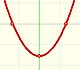
Polynomials of degree 2 are quadratic functions. Their graphs are parabolas. To find the x-intercepts we have to solve a quadratic equation. The vertex of a parabola is a maximum of minimum of the function.
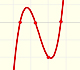
Polynomials of degree 3 are cubic functions. A real cubic function always crosses the x-axis at least once.
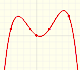
We can consider the polynomial function that passes through a series of points of the plane. This is an interpolation problem that is solved here using the Lagrange interpolating polynomial.

Podemos modificar las multiplicidades del cero y del polo de estas funciones sencillas.

Una primera aproximación a estas transformaciones. Representación de dos haces coaxiales de circunferencias ortogonales.
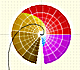
The Complex Exponential Function extends the Real Exponential Function to the complex plane.
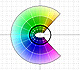
The Complex Cosine Function extends the Real Cosine Function to the complex plane. It is a periodic function that shares several properties with his real ancestor.

The Complex Cosine Function maps horizontal lines to confocal ellipses.
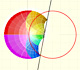
Inversion is a plane transformation that transform straight lines and circles in straight lines and circles.

Inversion preserves the magnitud of angles but the sense is reversed. Orthogonal circles are mapped into orthogonal circles

The usual definition of a function is restrictive. We may broaden the definition of a function to allow f(z) to have many differente values for a single value of z. In this case f is called a many-valued function or a multifunction.
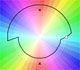
Multifunctions can have more than one branch point. In this page we can see a two-valued multifunction with two branch points.

The complex exponential function is periodic. His power series converges everywhere in the complex plane.

The power series of the Cosine Function converges everywhere in the complex plane.

We will see how Taylor polynomials approximate the function inside its circle of convergence.

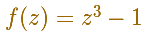

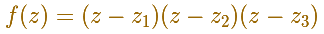




 PREVIOUS
PREVIOUS

























 NEXT
NEXT








