The tetrahedron is a regular pyramid. We can calculate its volume using a well known formula: The volume of a pyramid is one third
of the base area times the perpendicular height.
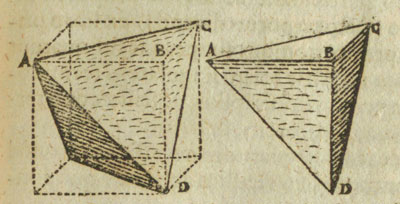
But we are going to make a construction that will help us to deduce easily the volume of a tetrahedron. Kepler showed us how to do that.
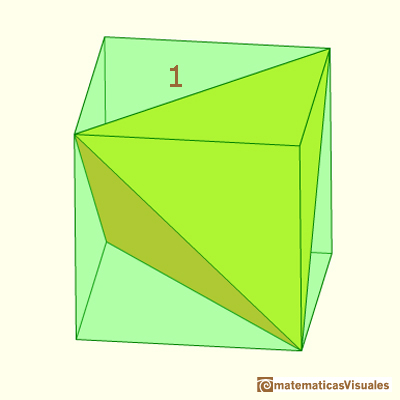
The idea is to build a tetrahedron inside of a cube.
Taking two diagonals of two opposite sides of a cube and attaching them properly we get a tetrahedron.
We want to see that the volume of the tetrahedron is one third of the cube that contains it.
If the tetrahedron edge length is 1 then the cube edge length w is:
We can write the volume of a cube with diagonal 1 (as a function of its wedge):
We can calculate this volume:
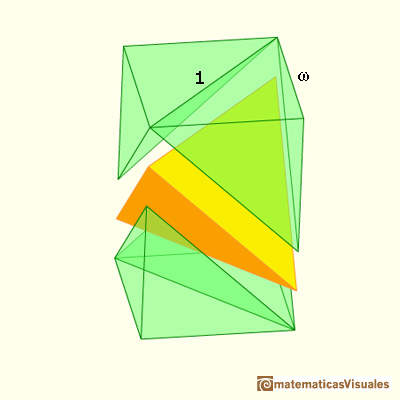
This cube is made of one yellow tetrahedron and four green pyramids.
The base of two of these pyramids is the base of the cube.
Then the volume of two pyramids (using the formula of the volume of a pyramid: one third of the base area times the height) is one third
of the volume of the cube.
The volume of these four green pyramids is two thirds of the volume of the cube. Then the volume of the yellow tetrahedron is one third.
We can see that the volume of the tetrahedron is one third of the cube that contains it.
Then, the volume of a tetrahedron with edge length 1 is:
The volume of a tetrahedron with edge length a is:
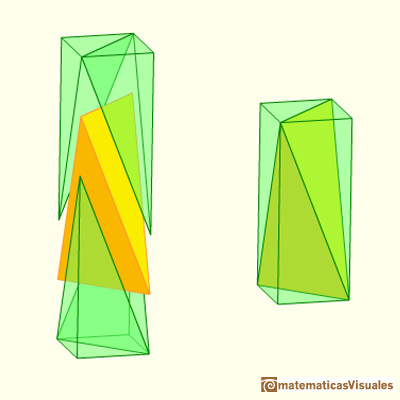
This construction can be generalized to any parallelepiped and we get not regular "tetrahedra" .
The volume of one of these tetrahedra is one third of the parallelepiped that contains it.
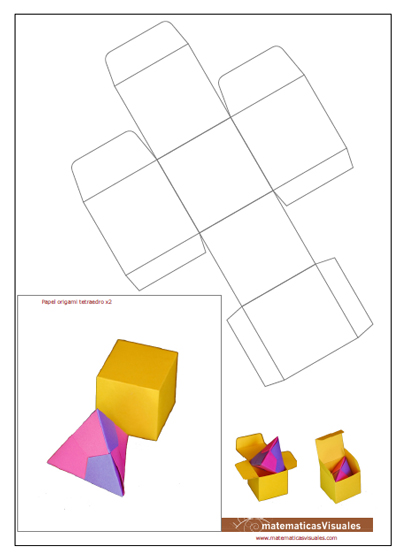
We can build a tetrahedron using modular origami and a cardboard cubic box.
This is a template for a cubic box to download. The rectangle is the paper size you need to build a tetrahedron that fit inside the cubic box:
You can see more examples of modular origami in Resources: Modular Origami
A container:
A tetrahedron made with four balls:
In Rothenburg ob der Tauber (Germany):
Tensegrity:
You can see more examples of tensegrity in Resources: Tensegrity
More origami: octahedron and tetrahedron.
Five tetrahedra in a dodecahedron:
REFERENCES
Hugo Steinhaus - Mathematical Snapshots - Oxford University Press - Third Edition (p. 197)
Magnus Wenninger - 'Polyhedron Models', Cambridge University Press.
Magnus Wenninger - 'Dual Models', Cambridge University Press.
Peter R. Cromwell - 'Polyhedra', Cambridge University Press, 1999.
H.Martin Cundy and A.P. Rollet, 'Mathematical Models', Oxford University Press, Second Edition, 1961 (p. 87).
W.W. Rouse Ball and H.S.M. Coxeter - 'Matematical Recreations & Essays', The MacMillan Company, 1947.
Luca Pacioli - De divina proportione - (La divina proporción) Ediciones Akal, 4ª edición, 2004. Spanish translation by Juan Calatrava.
MORE LINKS
We can cut in half a cube by a plane and get a section that is a regular hexagon. Using eight of this pieces we can made a truncated octahedron.

Demonstration of Pythagoras Theorem inspired in Euclid.

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Using eight half cubes we can make a truncated octahedron. The cube tesselate the space an so do the truncated octahedron. We can calculate the volume of a truncated octahedron.

These polyhedra pack together to fill space, forming a 3 dimensional space tessellation or tilling.
The truncated octahedron is an Archimedean solid. It has 8 regular hexagonal faces and 6 square faces. Its volume can be calculated knowing the volume of an octahedron.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

The stellated octahedron was drawn by Leonardo for Luca Pacioli's book 'De Divina Proportione'. A hundred years later, Kepler named it stella octangula.

Using cardboard you can draw plane nets and build polyhedra.

A very simple technique to build complex and colorful polyhedra.

Using cardboard you can build beautiful polyhedra cutting polygons and glue them toghether. This is a very simple and effective technique. You can download several templates. Then print, cut and glue: very easy!

Examples of polyhedra built using tubes.

Modular Origami is a nice technique to build polyhedra.

Examples of polyhedra built using tensegrity.

Examples of polyhedra built using Zome.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the truncated octahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the stellated octahedron (stella octangula).
In his article 'Two Surprising Theorems on Cavalieri Congruence' Howard Eves describes an interesting tetrahedron. In this page we calculate its cross-section areas and its volume.
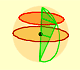
We want to calculate the surface area of sections of a sphere using the Pythagorean Theorem. We also study the relation with the Geometric Mean and the Right Triangle Altitude Theorem.

Howard Eves's tetrahedron is Cavalieri congruent with a given sphere. You can see that corresponding sections have the same area. Then the volumen of the sphere is the same as the volume of the tetrahedron. And we know how to calculate this volumen.

Special sections of a tetrahedron are rectangles (and even squares). We can calculate the area of these cross-sections.

Kepler used an intuitive infinitesimal approach to calculate the area of a circle.
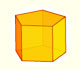
We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.
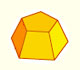
Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

Plane developments of cones and conical frustum. How to calculate the lateral surface area.
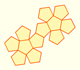
The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .




















 NEXT
NEXT