The Pythagorean Theorem (or Theorem of Pythagoras) is one of the most famous theorems of Mathematics. It is a property of right-angled triangles.
A right triangle or right-angled triangle is a triangle in which one angle is a right angle (angle C in the figure).
The right angle of a right-angled triangle has two legs and the opposite side is called the hypotenuse (side c in the figure).
Leg a is the side opposed (or opposite) to angle A and leg b is the side opposed to angle B in the illustration. This is a very typical notation.
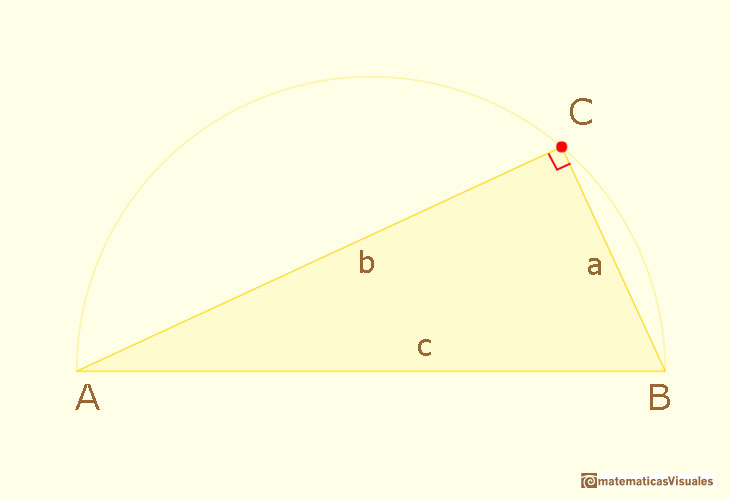
We notice that point C is always in a circle, the circumscribed circle. The diameter of this circle is the hypotenuse. This is a very interesting property and you can explore a demonstration of that fact in the next link:
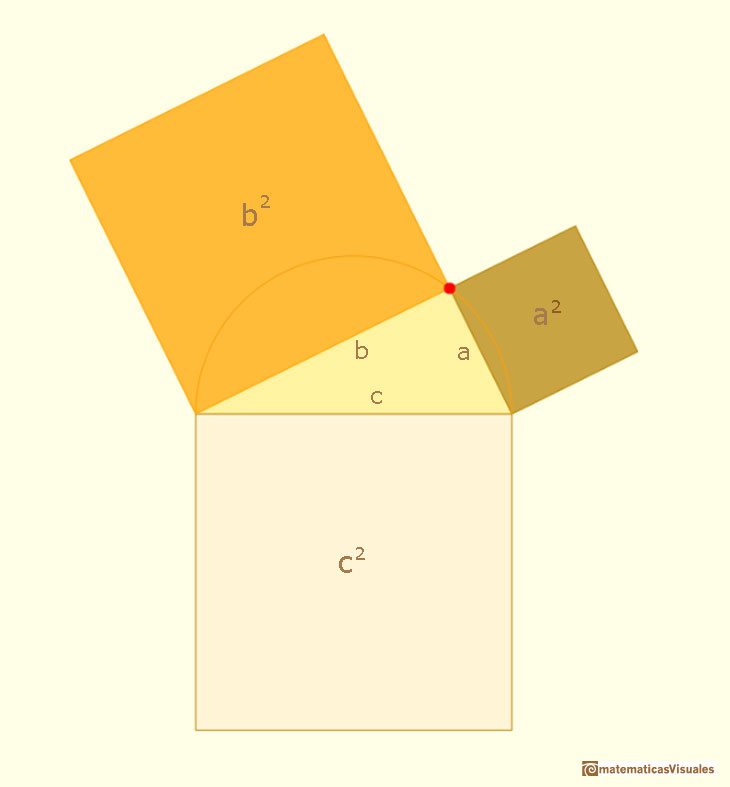
Then the Theorem of Pythagoras states that the square on the hypotenuse equals the sum of the (areas of the) squares on the other two sides.
The theorem says that the large square has the same area as the small and medium squares combined.
Here we can interact with a dynamic and interactive demonstration of the Pythagorean Theorem inspired in Euclid.
Euclid used triangles instead of parallelograms. You can see a typical representation of this theorem and Euclid's demonstration in a the next photos taken in Berlin.


Here we use the idea that if a parallelogram is changed by a shearing (preserving its base and altitude), its area remains constant.
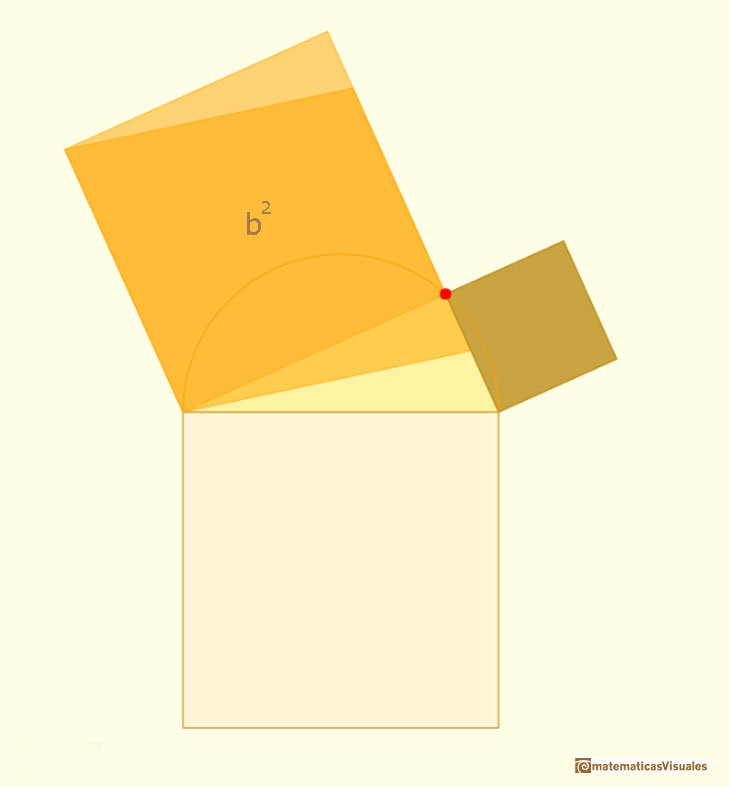
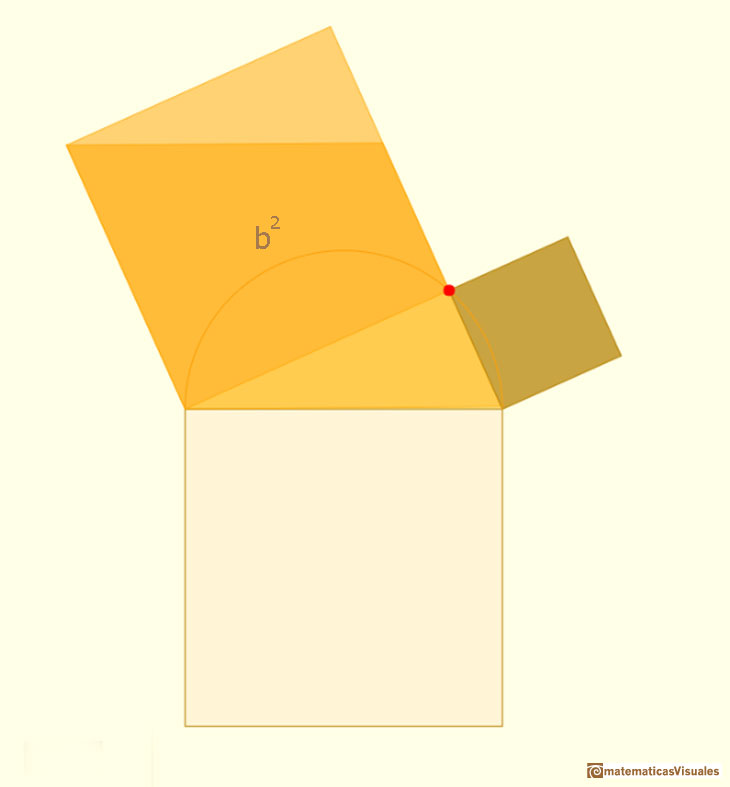
And if we consider a movement (a rotation in this case) of a parallelogram the area does not change.
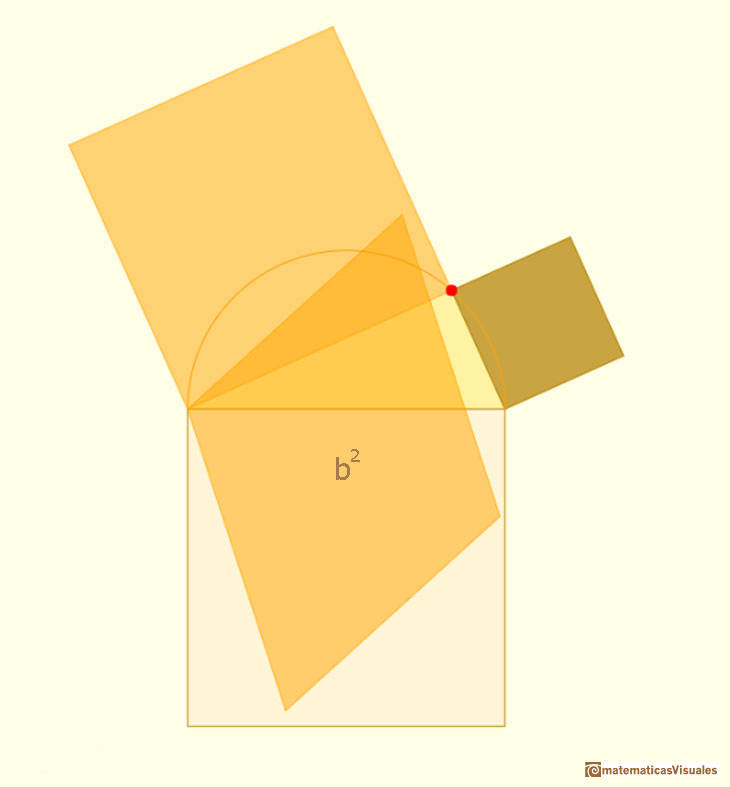
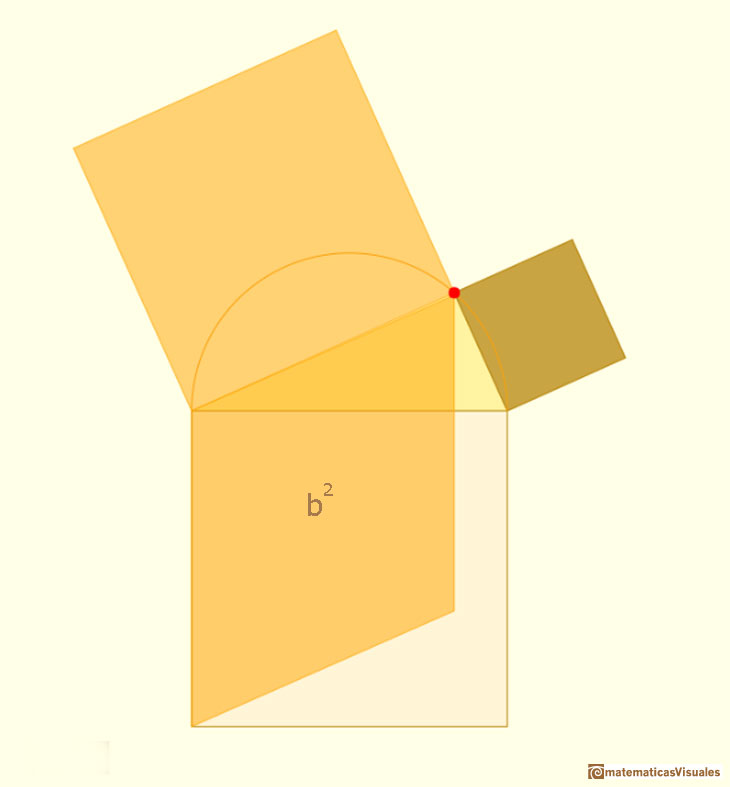
Another shearing:
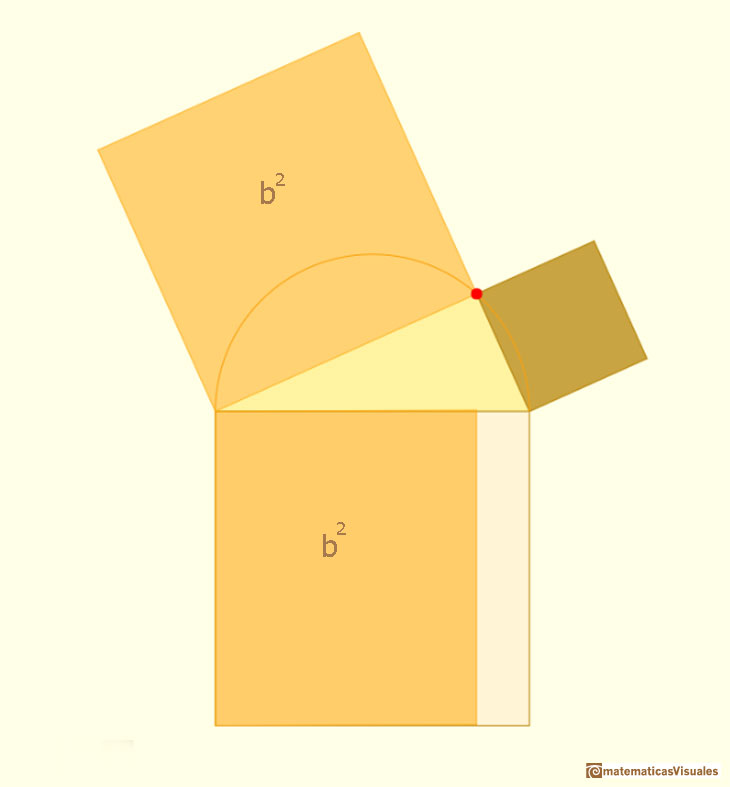
Is the same with the leg a.
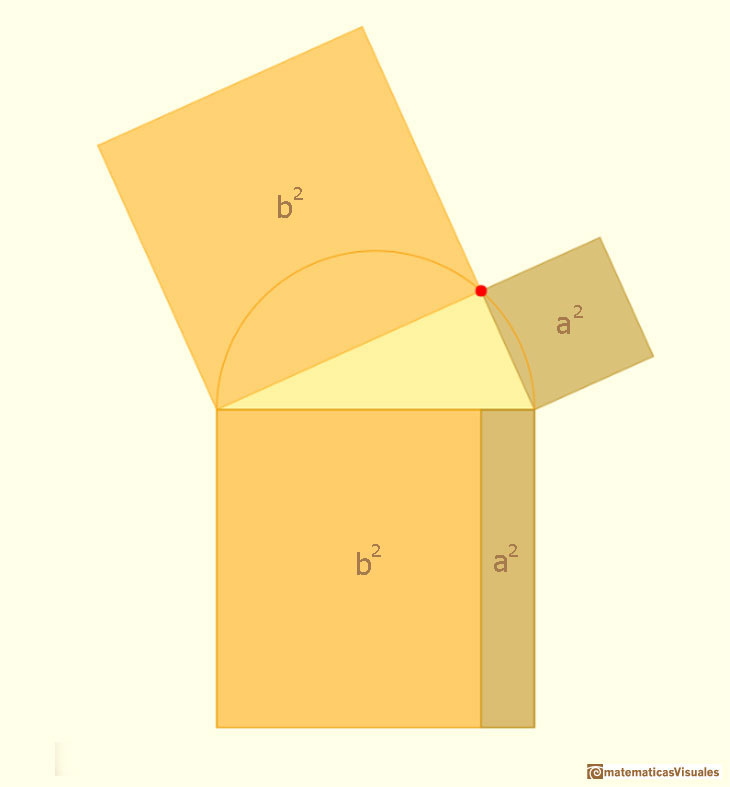
Then we have prove the Phitagorean Theorem:
We can see another property of right triangles.
In a right triangle, the altitude drawn from the right angle to the hypotenuse divides the hypotenuse into two segments.
These two segments are the projection of the two legs on the hypotenuse. Here we use the notation a' and b'.
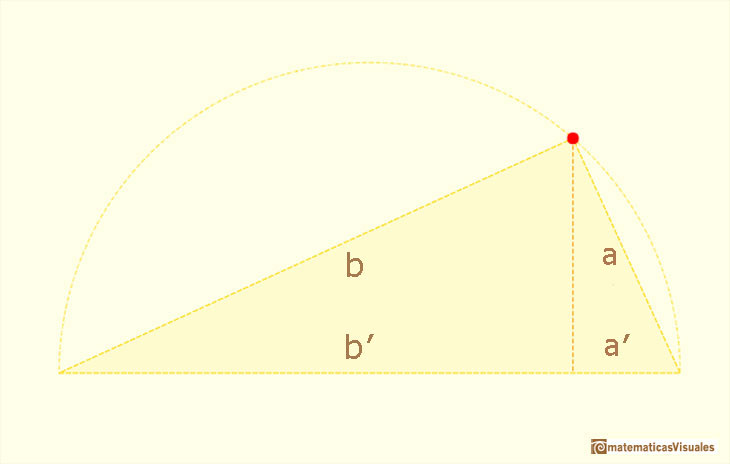
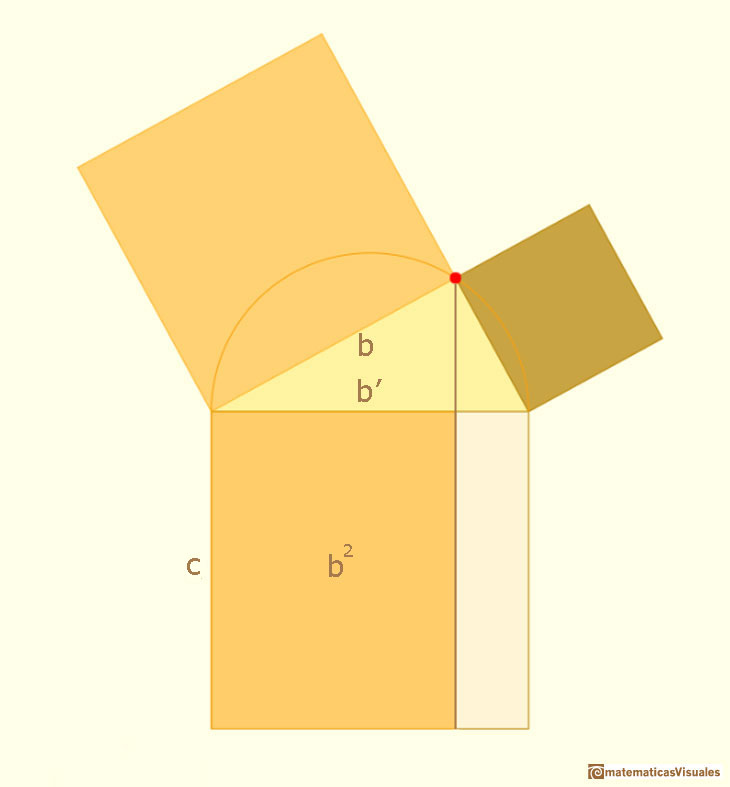
Then
We do not need the Pythagorean Theorem to prove this result. We can deduce it only using similarity.
The altitude to the hypotenuse of a right triangle forms two triangles that are similar to each other and to the original triangle.
Try to prove this result only using similarity.
We can use the concept of geometric mean and then this result can be written:
The length of each leg of the right triangle is the geometric mean of the lengths of the hypotenuse and the segment of the hypotenuse that is adjacent to the leg.
If you want to learn more about similarity and the geometric mean you can follow the next link:
One of the simplest right triangles has sides 3, 4 and 5, three integer numbers.
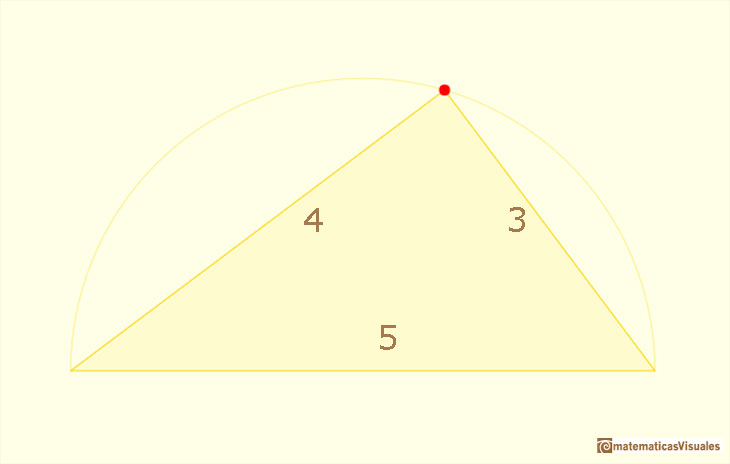
Integer triples like 3,4,5 are known as Pythagorean triples.
We can close this page with a citation from Stillwell:
"In is thought that in ancient times such solutions may have been used for the construction of right triangles. For example, by stretching a closed rope with 12 equally spaced knots one can obtain a (3, 4, 5) triangle with right angle between the sides 3, 4.
Whether or not this is a practical method for constructing right angles, the very existence of a geometric interpretation of a pure arithmetical fact like
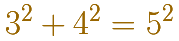
is quite wonderful. At first sight, arithmetic and geometry seem to be completely unrelated realms. Arithmetic is based on counting, the epitome of a discrete (or digital) process. The facts that arithmetic can be clearly understood as outcomes of certain counting processes, and one does not expect them to have any meaning beyond this. Geometry, on the other hand, involves continuous rather than discrete objetcs, suchs as lines, curves, and surfaces. Continuouos objects cannont be built from simple elements by discrete processes, and one expects to see geometrical facts rather tan arrive at them by calculation.
Pythagoras' theorem was the first hint of a hidden, deeper relationship between arithmetic and geometry, and it has continued to hold a key position between these two realms throughout the history of mathematics. This has sometimes been a position of cooperation and sometimes one of conflict, as followed the discovery that the square root of 2 is irrational. Is it often the case that new ideas emerge from such areas of tension, resolving the conflict and allowing previously irreconciliable ideas to interact fruitfully. The tension between arithmetic and geometry is, without doubt, the most profound in mathematics, and it has led to the most profuond theorems. Pythagoras' theorem is the first of these, and the most influential." (Stillwell)
REFERENCES
MORE LINKS

















 NEXT
NEXT