A cone is a geometric body consisting of a plane base bounded by a closed curve (the directrix) and every point of this curve is joined to a fixed point (the apex or vertex) lying outside the plane of the base. A pyramid is a special case of a cone with a polygonal base. If the directrix is a circle and the apex is perpendicularly above the center of the circle then the cone is a right circular cone. Then the cone has a rotational symmetry around the straight line passing through the apex (the axis of the cone). Each of the line segments between the apex and the base circle is a generatrix.

The main interest of this page is to see how right circular cones can be developed into a plane.

This is a right circular cone:

The cone developing into a plane:

This is a plane development of a cone:

To calculate the lateral surface area of a cone we need the slant height. The slant height is the distance from the base circle to the apex of the cone (the generatrix as a segment). There is a relation between the slant height and the height of a cone (Pythagorean theorem).

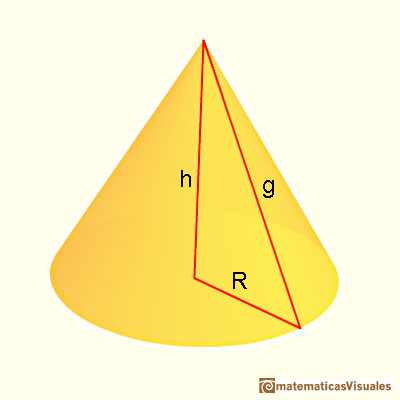
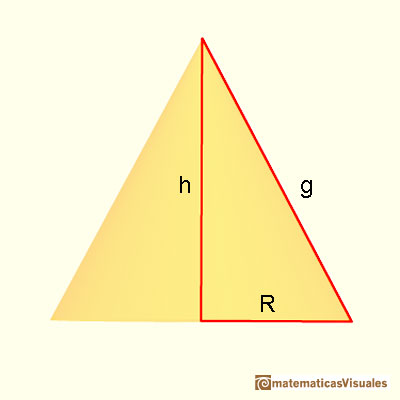
We are going to calculate the lateral surface area of a cone that is the area of a circular sector. If R is the base radius, the formula for the lateral surface area of a cone is like the formula for the area of a triangle. (The intuitive reason is like Kepler in Kepler and the area of a circle):

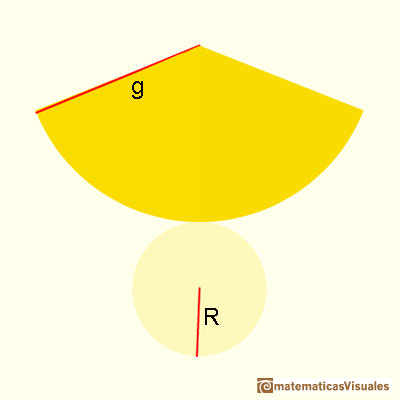
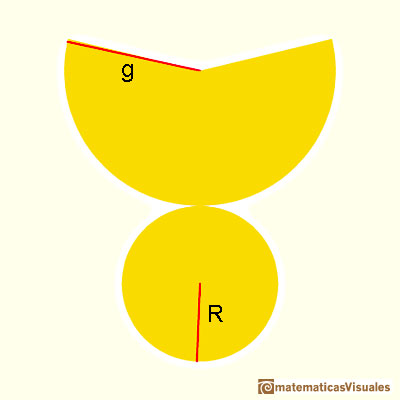
Do you remember the formula for the volume of a cone?

A cone with its apex cut off by a plane is called a truncated cone. If this truncation plane is parallel to the base then the body is called a conical frustum.

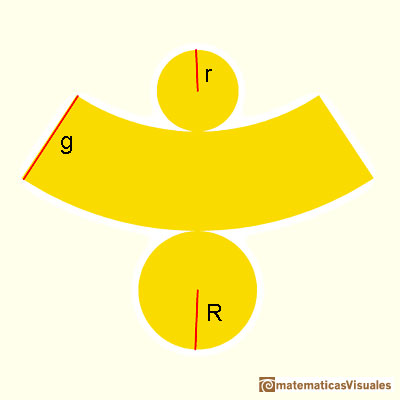
For example, this is a conical frustum:

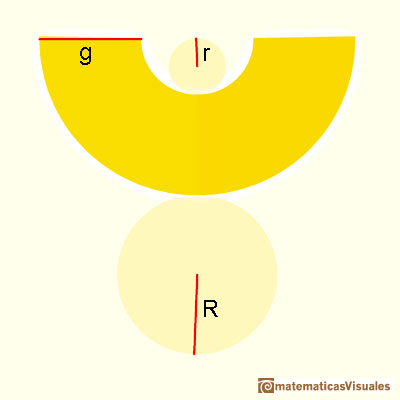
A conical frustum developing into a plane:

And this is its plane development:

As before, we need the slant height to calculate the lateral surface area of a frustum:

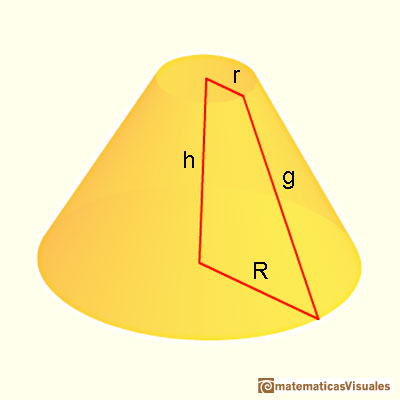
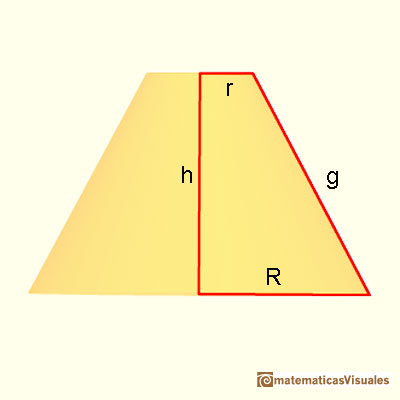
We can think, intuitively, that a cylindrical frustum is like a pyramidal frustum "with an infinite number of lateral faces". This is a very imprecise way of thinking that can remind us the origins of the Calculus, like Kepler's era. We can remind that the formula for the lateral surface area of a pyramidal frustum is like the area of a trapezoid (lateral faces are congruent trapezoids). When we calculate the lateral surface area of a conical frustum, the formula reminds us the formula for the trapezoid again:

Door in Peñalba de Santiago (León, Spain, July 2016)

MORE LINKS

Plane developments of geometric bodies (5): Pyramid and pyramidal frustrum

Plane net of pyramids and pyramidal frustrum. How to calculate the lateral surface area.

Plane developments of geometric bodies (4): Cylinders cut by an oblique plane

We study different cylinders cut by an oblique plane. The section that we get is an ellipse.

Plane developments of geometric bodies (3): Cylinders

We study different cylinders and we can see how they develop into a plane. Then we explain how to calculate the lateral surface area.

Ellipses as sections of cylinders: Dandelin Spheres

The section of a cylinder by a plane cutting its axis at a single point is an ellipse. A beautiful demonstration uses Dandelin Spheres.

Albert Durer and ellipses: cone sections.

Durer was the first who published in german a method to draw ellipses as cone sections.

Albert Durer and ellipses: Symmetry of ellipses.

Durer made a mistake when he explanined how to draw ellipses. We can prove, using only basic properties, that the ellipse has not an egg shape .

Plane developments of geometric bodies (2): Prisms cut by an oblique plane

Plane nets of prisms with a regular base with different side number cut by an oblique plane.

Plane developments of geometric bodies (1): Nets of prisms

We study different prisms and we can see how they develop into a plane net. Then we explain how to calculate the lateral surface area.

Plane developments of geometric bodies: Dodecahedron

The first drawing of a plane net of a regular dodecahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Plane developments of geometric bodies: Octahedron

The first drawing of a plane net of a regular octahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Plane developments of geometric bodies: Tetrahedron

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Cavalieri: The volume of a sphere

Using Cavalieri's Principle we can calculate the volume of a sphere.

The volume of the tetrahedron

The volume of a tetrahedron is one third of the prism that contains it.

Plane developments of geometric bodies: Tetrahedron

The first drawing of a plane net of a regular tetrahedron was published by Dürer in his book 'Underweysung der Messung' ('Four Books of Measurement'), published in 1525 .

Volume of an octahedron

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

Chamfered Cube

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.

Resources: How to build polyhedra using paper and rubber bands

A very simple technique to build complex and colorful polyhedra.