Albrecht durer (1471-1528) was a German painter and engraver. He was one of the greatest artist of the Northern Renaissance. He traveled to Italy where he met Jacobo de Barbari and he was aware of the works of Pacioli. He was a great admirer of Leonardo da Vinci. He learned from Barbari a lot about the new developments in perspective and and the theory of proportions (About Dürer's interest in mathematical transformation you can see durer and transformations of faces).
Dürer studied mathematics and mastered perspective through his study of geometry. He read and recomended to study Euclid. He thought that the study of geometry was indispensable for the study of the arts.
In 1525 Dürer published the first mathematical book in German, the "Four Books on Measurement" or "Course in the Art of Measurement with Compass and Ruler". (Underweysung der Messung mit dem Zirckel und Richtscheyt). In this book he wrote about a large number of curves, how to draw some polygons. He considers pyramids, cylinders and other solids bodies, sundials and other astronomical instruments. He studied the five Platonic solids and several Archimedean solids and he drew nets of these polyhedra. He also introduces the theory of perspective and describes several apparatuses to transfer an object to a drawing sheet from a specific point of view.
In his book "The Life and Art of Albrecht Dürer", Panofsky pointed out the importance of this book: "Apart from this technical inventio Dürer added nothing to the science of perspective as developed by the Italians. Yet the las section of his 'Unterweisung der Messung' is memorable in two respects. First, it is the first literary document in which a strictly representational problem received a strictly scientific treatment at the hands of a Northerner; none of Dürer's forerunners and few of his contemporaries had any understanding of the fact that the rules for the construction of a perspective picture are based on the Euclidian concept of the visual pyramid or cone (...). Second, it emphasizes (...) that perspective is not a technical discipline destined to remain subsidiary to painting or architecture, but an important branch of mathematics, capable of being developed into what is now known as general projective geometry." (Erwin Panofsky, The Life and Art of Albrecht Dürer, p. 253).
"The 'Unterweisung' is, therefore, still a book for practical use and not a treatise on pure mathematics. Dürer wanted to be understood by artists and artisans".(Erwin Panofsky, The Life and Art of Albrecht Dürer, p. 254). His main interest was the applicability of these geometric techniques to artist and craftsmen.
One of the most interesting features of the First Book is the first discussion in German of conic sections.
Greek mathematicians had interest in conic sections (Archimedes, Apollonius of Perga), ellipses in particular. In matematicasVisuales you can find information about ellipses.
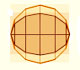
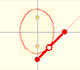
An ellipse is commonly defined as the locus of points P such that the sum of the distances from P to two fixed points F1, F2 (called foci) are constant. We are going to use this definition later.
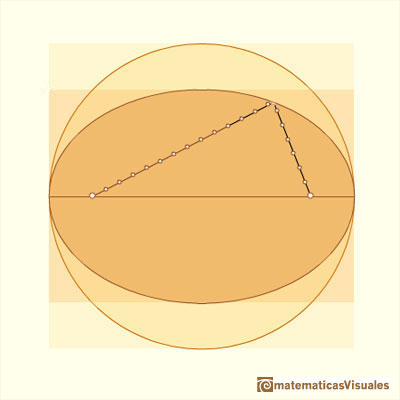
We know how to calculate the area of the ellipse:

Even we can build mechanical devices to draw ellipses:
Ellipses were very important for painters because they know that every circle seems an ellipse when is viewed from an oblique point of view.
For example, you can see several fragments of paintings with ellipses that you can find in Museo Thyssen-Bornemisza in Madrid, .
Dürer's approach was original. "Instead of investigating the mathematical properties of the parabola, hyperbola and ellipse, he tried to construct them just as the had tried to construct his spirals and epicycloids; and this he achieved by the ingenious application of a method familiar to every architect and carpenter, but never before applied to the solution of a purely mathematical problem, the method of parallel projection. He represented the cone, cut as the case may be, in side elevation and groundplan and transferred a sufficient number of points from the former into the latter." (Erwin Panofsky, The Life and Art of Albrecht Dürer, p. 254-255).
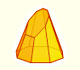
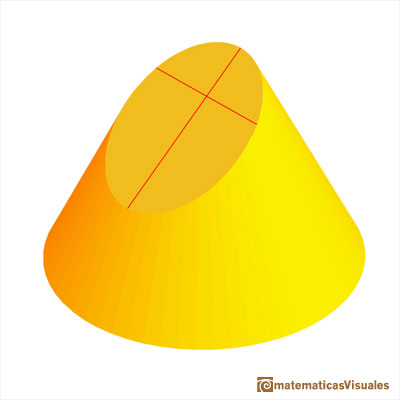
Then his method uses a side view and a view from above of a cone cut by an oblique plane.
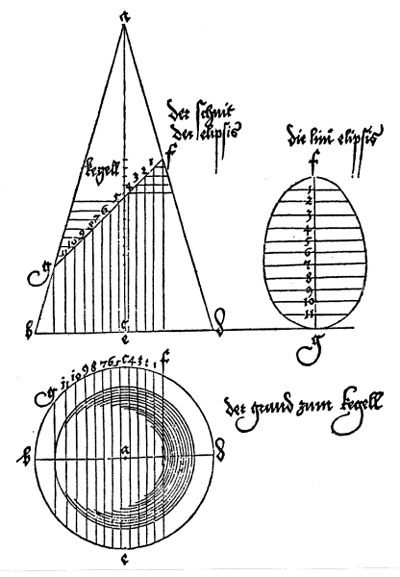
We can start drawing the major axis of the ellipse:
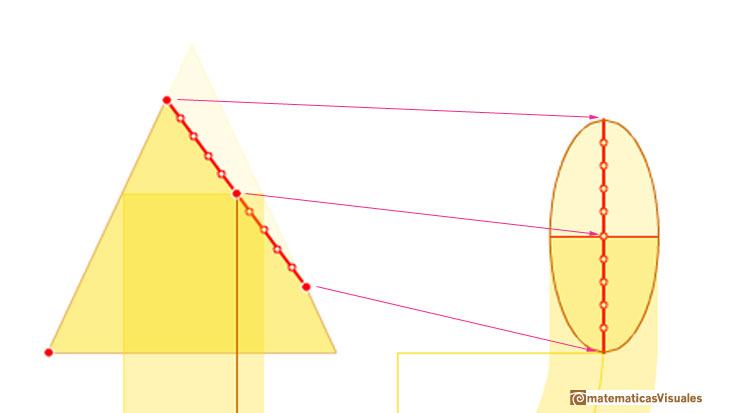
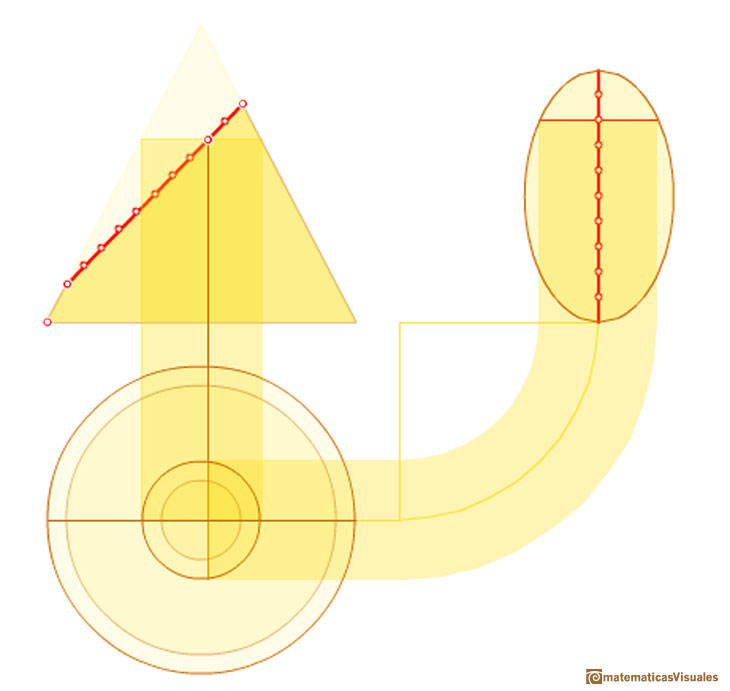
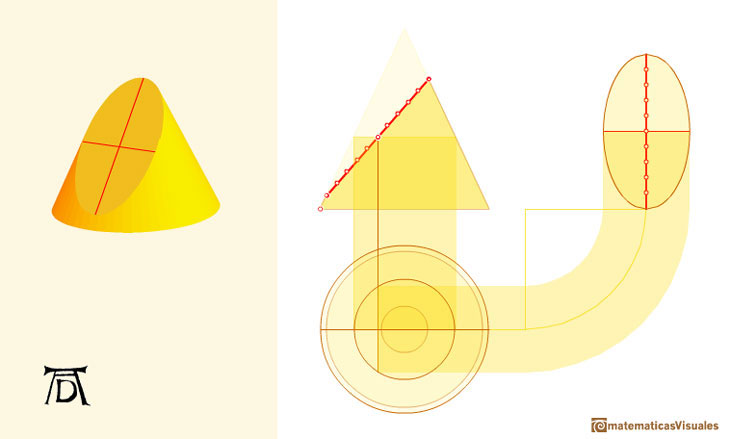
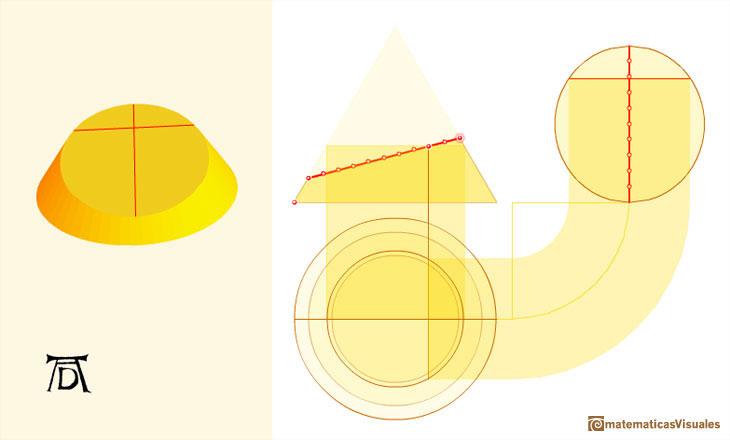
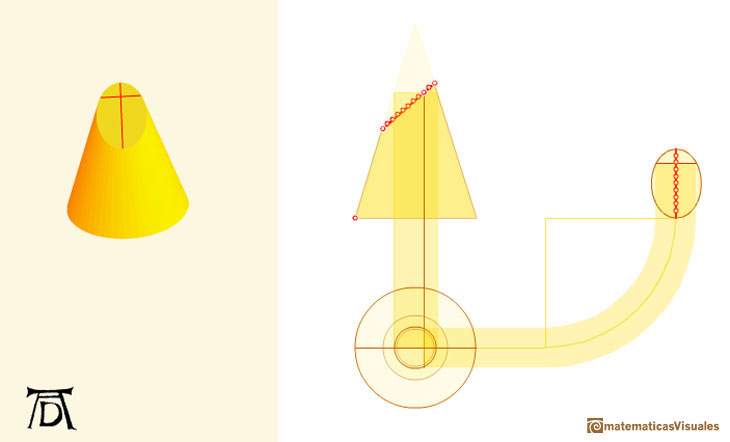
A circle is a particular case of an ellipse:
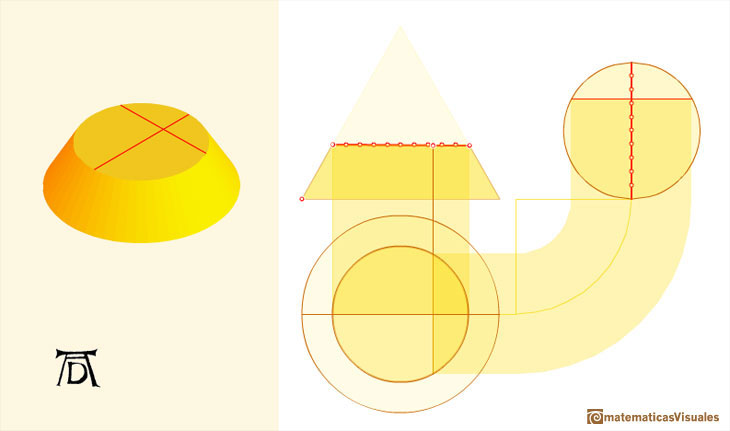
"Crude though it is, this method, which may be called a genetic as opposed to a descriptive one, announces, in a way, the procedure of analytical geometry and did not fail to attract the attention of Kepler who, with a smile, refers to the only mistake in Dürer's analysis. Like any schoolboy, Dürer found it hard to imagine that an ellipse is a perfectly symmetrical figure. He was unable to get away from the idea that it should widen in proportion with the widening of the cone, and he involuntarily twisted the construction until it resulted, not in an orthodox ellipse but in an 'Eierlinie' ('egg line'), narrower at the top that at the bottom. Even with Dürer's primitive methods the error could have been easily avoided. That it was committed, not only illustrates a significant conflict between abstract geometrical thought and visual imagination, but also proves the independence of Dürer's researches." (Erwin Panofsky, The Life and Art of Albrecht Dürer, p. 255).
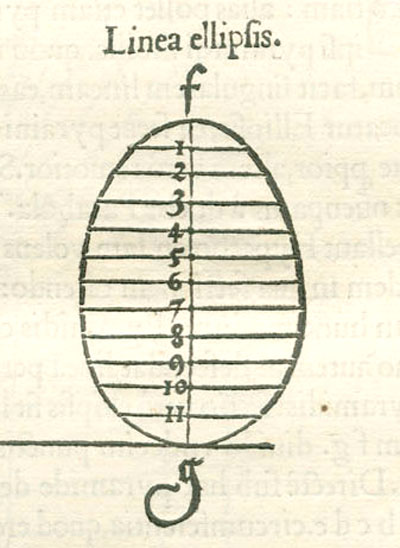
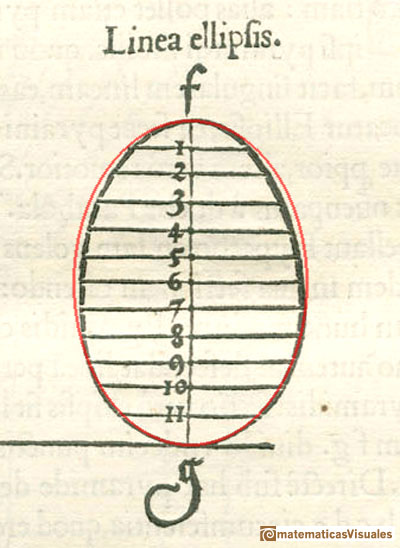
DISCUSSION
But, are we sure that Dürer behaved 'like any schoolboy', as Panofsky wrote? Who knows what a genius like Dürer was thinking?
Some relevant mathematicians who have studied Dürer's works think differently.
Dan Pedoe, in his book 'Geometry and the Liberal Arts' wrote "I am not convinced that Dürer was misled".
Dirk Huylebrouck, in his article '500 Years of Melancholia' thinks that "there is no proof at all Dürer thought an elliptic intersection gets broader where the cone gets broader. He never said so".
Following the next link you will find more details about Pedoe and Huylebrouck opinions.
And a question for you, could you prove, using only basic Mathematics, that ellipses as a conic section have two symmetry axis?
I made this construction using bowls, magnets, a steel ball, plastic and methacrylate:







Following Stanley Ogilvy's book 'Excursions in Geometry' we are going to see that this kind of section of a cone is an ellipse because it verifies the locus definition of an ellipse: points of an ellipse are such that the sum of its distances from two fixed points (foci of the ellipse) is constant. The demonstration is similar to that of the Ellipses as sections of a cylinder: Dandelin Spheres.
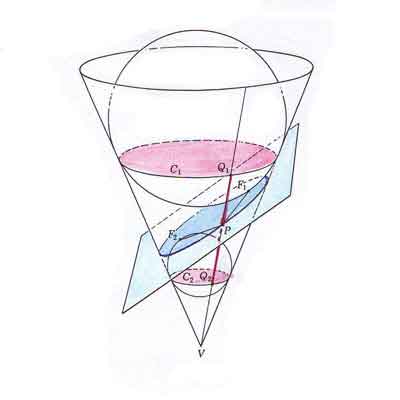
"Fig. 60 there is just one sphere, called a Dandelin sphere after the invertor of this proof, that would fit snugly into the cone and also be tangent to the upper surface of the cutting plane, say at some point F1. A second Dandelin sphere is tangent to the cone and to the plane at F2. These two points will turn out to be the foci of the ellipse.
Select any point P on the curve and draw PV. Because P is on the cone, the straight line element PV not only cuts circles C1 and C2, but also is tangent to the two spheres, at Q1 and Q2. But PF1 and PF2 are also tangent lines to the spheres, because they lie in the tangent plane. Now tangents to any one sphere from an external point are equal. That is,
Adding,
Now let P move around the ellipse. There will be a new Q1 and a new Q2 for each position of P, but the length Q1Q2 remains constant (why?). Thus
the definition of an ellipse with foci at F1 and F2.
Tom Apostol referred to this demonstration as the 'ice-cream-cone proof'.
A beach ball rests on the floor, illuminated by a single electric light. What is the shape of the ball's shadow on the floor? Where does the ball touch the floor?" (Ogilvy, "Excursions in Geometry", p. 80-81).




REFERENCES
 NEXT
NEXT
 PREVIOUS
PREVIOUS
MORE LINKS