
The principal goal of this article is to show Kepler's contributions to the development of calculus in a visual and interactive way.
During the century before Newton and Leibniz the works of Greek mathematicians were popular, especially the work of Archimedes. Infinitesimal techniques were developed for calculating areas and volumes, and Johannes Kepler (1571-1630) contributed to these developments. His interest in calculating areas and volumes stemmed from an incident that occurred when he married for the second time in Linz, Austria. Kepler had purchased a barrel of wine for the wedding and the wine merchant’s method of measuring the volume at first angered him. This inspired Kepler to study how to calculate areas and volumes and to write a book about the subject, Nova stereometria doliorum vinariorum (New solid geometry of wine barrels), in 1615, which was his main contribution to the development of integral calculus.
The wine barrel incident also led Kepler to take up another problem of differential calculus, the problem of maximums: What is the best design for a barrel in order to maximize its volume? Today, we solve this problem using derivatives because we know that, at a maximum (or minimum) value of a differentiable function, the derivative of a function is zero. Fermat was the first to relate maximum and minimum problems to tangents of curves: at a maximum or a minimum the slope of the tangent of the function is zero. Kepler was able to show that, despite minor differences, the proportions of the Austrian wine merchant's barrels were such that the procedure used to calculate the volume actually would be quite accurate, after all.
Johannes Kepler (1571 – 1630) was a German mathematician, astronomer, and astrologer, and a key figure in the 17th century scientific revolution. He lived after Copernicus and supported the heliocentric model of the universe. Kepler worked with Tycho Brahe and used Brahe's remarkable observational data to make his most famous discovery, the three laws of planetary motion now known as Kepler's Laws. Newton later showed that Kepler's laws could be deduced from Newton's laws of motion and universal gravitation law.
As a mathematician Kepler discovered two new regular polyhedra, worked on the problem of close packing of equal spheres, was interested in logarithms and found volumes of solids of revolution.
Our main purpose here is to understand Kepler's contributions to the development of calculus.
Kepler lived before Newton and Leibniz. During the sixteenth century and early seventeenth century, the Greek mathematical masterworks, such us Euclid's Elements, the Conics of Apollonius or the works of Archimedes, were studied seriously. Numerous mathematicians refined the method of exhaustion and applied it to a wide variety of new quadrature (area) and cubature (volume) problems. Another point of interest was the determination of centers of gravity of solids (see Margaret Baron's book p. 90 about the importance of centers of gravity for the development of the calculus). Renaissance mathematicians were more interested in new results and methods of discovery than in rigorous proofs. They freely used intuitive concepts of the infinite to produce infinitesimal methods for the solution of area and volume problems. Kepler and Cavalieri were two key mathematicians who helped invent these infinitesimal methods.
Kepler had several children before his first wife died. In 1613, he married for the second time in a celebration in Linz, Austria. Kepler bought a barrel of wine for the wedding but questioned the method the wine merchant used to measure the volume of the barrel and thus determine the price.
In consequence, afterwards Kepler set out both to determine the correct volume of a wine barrel or cask, and to find the proportions that optimize the wolume of a wine cask.
You can see the whole book "Nova Stereometria doliorum vinariorum" in The Posner Library)
The drawing at right of a wine barrel lying on its side shows how the wine merchant determined the volume of the barrel, and thus the price of the wine. The merchant would insert a stick through the tap hole (at center top in the drawing) to the opposite edge of the lid of the barrel (at lower left or lower right). The length of stick inserted into the barrel determined the price the merchant would charge!
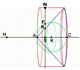
To determine the volume of a wine barrel accurately, Kepler thought of the volume of the cask, or of any solid body, as made up of numerous thin sheets suitably ranged in layers, and treated the volume as the sum of the volumes of these leaves, each of which was a cylinder. (Klein, p. 209)
The animation below shows how Kepler could refine his approximation by using more and more cylinders. These cylindrical slices are taken perpendicular to the axis of the barrel. Each diameter is equal to that of the barrel at that particular height. The height of each cylinder could be as thin as we can imagine. These cylindrical slices are piled one on top of the other. All together constitute the barrel.
According to Otto Toeplitz (p.83):"Working out finer approximations of various barrel shapes, he consulted Archimedes and discovered that his own method of indivisibles had enabled him to obtain results in a far simpler and more general way than Archimedes, who had been struggling with cumbersome and difficult proofs. What he did not suspect was that Archimedes, too, had found his results by the same method of indivisibles (for the Method was lost until 1906!)."
The reference to the Method is to the work by Archimedes where he describes how he found many of his results on areas and volumes. When an old manuscript of this book was discovered it was studied by Heiberg. Now this book is deposited at The Walters Art Museum in Baltimore and we can learn a lot about this fascinating work at Archimedes: The Palimpsest Project.
|
Archimedes' Method for Computing Areas and Volumes
Article by Gabriela Sanchis in Loci Convergence where she explains Archimedes' Method based on the Law of the Lever. |
|
Archimedes in MatematicasVisuales - Area of a parabolic segment
Archimedes used infinitesimal methods to discover areas an volumes 1800 years before Kepler or Cavalieri. |
Kepler reported his results on wine barrels in his 1615 book, Nova stereometria doliorum vinariorum (New solid geometry of wine barrels). The word Stereometria is from the Ancient Greek stereos that means solid or three-dimensional and metron that means a measure or to measure. Then Stereometria means the art of measuring volumes or solid geometry. From the title, we use Doliometry that is an old-fashioned word from the Latin dolium that means a large jar or barrel.
This book is a systematic work on the calculation of areas and volumes by infinitesimal techniques. Building on the work of Archimedes, it focuses on solids of revolution and includes calculations of exact or approximate volumes of over ninety such solids (Edwards, p. 102). Today we use integral calculus to solve these kinds of problems.

|
Original Latin version in The Posner Memorial Collection
Full book in The Posner Memorial Collection,Carnegie Mellon University Libraries, Pittsburgh PA Original German version in ConvergenceTwo pages of a original german version of Nova Stereometria. |
According to C.H. Edwards (p. 102), "Kepler's approach in [his Stereometria was] to dissect a given solid into an … infinite number of infinitesimal pieces, or solid 'indivisibles', of a size and shape convenient to the solution of the particular problem." Kepler then added up the volumes of the component pieces to obtain the volume of the given solid. Kepler's infinitesimal elements had to possess the same dimensions as the body he wanted to measure. That is, if he wanted to calculate an area, he added up area elements and if he wanted to calculate a volume he considered solid infinitesimal elements with volume.
Kepler opened his work on curvilinear measurement with the simple problem of determining the area of the circle. He regarded the circle as a regular polygon with an infinite number of sides and therefore composed of infinitely many infinitesimal triangles of which the bases were the sides of the polygon, the heights or altitudes the radius of the circle, and the vertices opposite the bases the center of the circle. Since the area of a triangle is one-half the product of its base and height, the total area was then given by half the product of the perimeter (or circumference) and the radius.

|
Kepler in MatematicasVisuales - The Area of a Circle
Kepler used an intuitive infinitesimal approach to calculate the area of a circle. |
Similarly, by thinking of the sphere as being composed of an infinite number of infinitesimal cones whose vertices were the center of the sphere and whose bases made up the surface of the sphere, Kepler was able to demonstrate that the volume of the sphere equals one-third the product of the surface area and the radius. (Recall that the volume of a cone is one-third the product of the area of its base and its height or altitude.)
Kepler also rotated a circle about a line external to the circle, and calculated, by infinitesimal methods, the volume of the torus thus generated. He then extended his work to solids not treated by the ancients. Some of his summations are remarkable anticipations of results found later in integral calculus.

|
Kepler in Mathworld: Lemon
Kepler in Mathworld: Apple In Mathworld we can see several solids of revolution defined by Kepler. |
The method the wine merchant had used to measure the volume of the barrel that had so shocked Kepler was to insert a stick through the tap hole (at S in the diagram below) to the opposite edge of the lid of the barrel (at D).
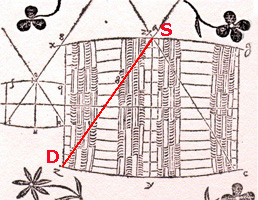
"Then he read off the length SD = d and set the price accordingly. This outraged Kepler who saw that a narrow, high barrel might have the same SD as a wide one and would indicate the same wine price, though its volume would be ever so much smaller" (Toeplitz, pp. 82-83).
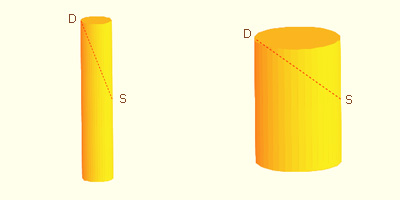
In consequence, Kepler tried to determine the best proportions for a wine barrel in order to maximize the volume. This brought him to the consideration of a number of problems on maxima and minima, which proved to be a very interesting contribution toward the development of differential calculus. For example, Kepler was able to establish that the cube is the greatest parallelepiped which can be inscribed in a sphere. (Baron, 115)
Of course, the problem of finding maxima and minima was not new. For example, Euclid had proven that among all rectangles of equal perimeter the square has the largest area (Toeplitz, 80). Pappus of Alexandria around 300 CE showed that, of all equilateral and equiangular plane figures having an equal perimeter, the figure with the greater number of angles has the greater area, and the largest such area is that of the circle with that same perimeter".

|
The Sagacity of Circles: A History of the Isoperimetric Problem
Article by Jennifer Wiegert in Convergence. A summary of the history of the problem of finding the region of greatest area bounded by a given perimeter. |

|
Thinking Outside the Box -- or Maybe Just About the Box
Article by David Meel and Thomas Hern in Convergence. They study a more complex and realistic box problem than the traditional one and show how it can be used to investigate optimization. |
To optimize the volume of the barrel, Kepler simplified the problem. He approximated the barrel by a cylinder with the diagonal measurement d as above, r the radius of the base, and h the height. In modern notation, the formula for the volume V of a cylinder is:
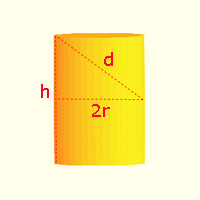
Then, a relation between d, h and r can be written using the Pythagorean Theorem:
Now solve for r squared:
Hence, we can deduce the formula of the volume as a function of h and d:
For fixed d, the following animation shows how the volume V changes when we modify the height h of the barrel.
Next, Kepler asked: "If d is fixed, what value of h gives the largest volume V?" (Toeplitz, p. 83). After making some calculations and comparing them, he decided the answer was:
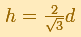
"That defined a barrel of definite proportions. Kepler noticed that in his Rhenish homeland barrels were narrower and higher than in Austria, where their shape was peculiarly close to that having a maximum volume for a fixed d - so close, indeed, that Kepler could not believe this to be accidental. So he imagined that centuries ago somebody had calculated barrel shapes, as he himself was doing, and had taught the Austrians to construct their barrels in this particular fashion - a very practical one, indeed. Kepler showed that if a barrel did not satisfy the exact mathematical specification
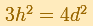
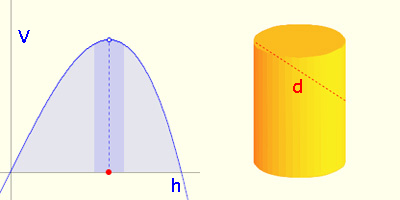
but deviated somewhat from it, this would have but little effect on the volume, because near its maximum a function changes only slowly" (Toeplitz, p. 83), as illustrated in the graph below.
Kepler tabulated values obtained by calculation to reinforce his idea that the volumes of such cylinders with equal diagonals change very little in the neighbourhood of a maximum. (Baron, p. 116)
This page and the whole book is available at The Posner Memorial Collection: Kepler, Nova Stereometria.
"Thus, while the Austrian method of price determination, if applied to Rhenish barrels, would be a clear fraud, it was quite legitimate for Austrian barrels. The Austrian shape had the advantage of permitting such a quick and simple method. So Kepler relaxed in this instance" (Toeplitz, p. 83).
This, then, was a major contribution by Kepler: He remarked that as the maximum volume was approached, the change in the volume for a given change in the dimensions became smaller. Some years later, Fermat would work on this kind of maximum and minimum problem with a different point of view.
Fermat (born in 1601) had a different approach: In modern terms, he was interested in the tangent to a curve and the relation between this tangent and the maximum (or minimum) of a function. He was the first to solve maximum-minimum problems by taking into account the characteristic behavior of a function near its extreme values.
Fermat's algebraic approach to this problem can be seen today as equivalent to studying the slope of the tangent to the curve representing the function. Newton and Leibniz had a clearer idea and they realized that a maximum or minimum was associated with a horizontal tangent.
Using our modern terminology, this is the geometric interpretation of the derivative of a function. We can see intuitively that if f(x) is a maximum (or minimum) value of the differentiable function f, then the value of f changes very slowly near x. Moreover, at the highest and lowest points on the graph of f the tangent is horizontal; that is, its slope is 0. The derivative will be zero at extrema.
Returning to Kepler's problem of the proportions of a wine barrel, if V is the volume of the barrel (as a cylinder) with a fixed value of d, then V is a polynomial in h; hence the derivative is easy to calculate:
For V to be a maximum, V' must equal zero; hence
And this was the result that Kepler found.
In the diagram below, the blue curve is the graph of y = V(h) and the red curve the graph of y = V'(h) for a fixed value of d.
Thus, the practical problem of measuring the volume of a wine barrel inspired Kepler to make important contributions to the development of both the integral and differential calculus.
Margaret E. Baron, The Origins of the infinitesimal Calculus, Dover Publications, New York, 1987.
Carl B. Boyer, The History of the Calculus and its Conceptual Development, Dover Publications, New York, 1959.
Roberto Cardil, Kepler: Doliometry, the volume of a barrel, and Kepler: Doliometría, el volumen de un tonel, MatematicasVisuales, posted 8-9 December 2009.
Roberto Cardil, Kepler: Volume of a Wine Barrel, MatematicasVisuales, posted 8 January 2010.
C.H. Edwards, The Historical Development of the Calculus, Springer-Verlag New York, 1979.
Felix Klein, Elementary Mathematics from an Advanced Standpoint. Arithmetic, Algebra, Analysis (p. 209), Dover Publications, New York, 2004.
Dirk J. Struik (ed.) , A Source Book in Mathematics, 1200-1800. Kepler. Integration Methods (pp. 192-197), Harvard University Press, Cambridge, MA, 1969.
Otto Toeplitz, The Calculus: A Genetic Approach (pp. 82-83), University Of Chicago Press, 1963.

|
Kepler in Mac Tutor History of Mathematics
A biography of Kepler. |

|
Original latin version in The Posner Memorial Collection (full book)
Original german version in Convergence (two pages) Original versions of Nova Stereometria available on the web. |

|
Kepler in MatematicasVisuales - The Area of a Circle
Kepler used an intuitive infinitesimal approach to calculate the area of a circle. |

|
Kepler in Mathworld: Lemon
Kepler in Mathworld: Apple In Mathworld we can see several solids of revolution defined by Kepler. |

|
Archimedes' Method for Computing Areas and Volumes
Article by Gabriela Sanchis in Loci Convergence where she explains Archimedes' Method based on the Law of the Lever. |

|
Archimedes in MatematicasVisuales - Area of a parabolic segment
Archimedes used infinitesimal methods to discover areas an volumes 1800 years before Kepler or Cavalieri. |

|
The Sagacity of Circles: A History of the Isoperimetric Problem
Article by Jennifer Wiegert in Convergence. A summary of the history of the problem of finding the region of greatest area bounded by a given perimeter. |

|
Thinking Outside the Box -- or Maybe Just About the Box
Article by David Meel and Thomas Hern in Mathdl. They study a more complex and realistic box problem than the traditional one and show how it can be used to investigate optimization. |
Roberto Cardil Ricol is a Secondary School teacher of Mathematics in Spain. He studied as a teacher (Huesca University, Spain), Bachelor in History (Barcelona University, Spain) and Bachelor in Mathematics (Zaragoza University, Spain). He has taught Mathematics to students from 6 years to the University. He maintains the site www.matematicasvisuales.com and enjoys the beauty of Mathematics.
I would like to thank Janet Beery, Convergence editor, for her support and encouragement. Without her help this article would not have been published.
I thank the anonymous referees for suggestions that improved the article.
I am grateful to the Posner Library for granting permission to use images from its copy of Kepler's Nova stereometria doliorum vinariorum in this article.
Miguel Cardil helped me in the artistic design of the page and has also designed all graphic elements in the mathlets.
I would like to thank Kathleen Killorin for her help in the English translation.