Matematicas Visuales | John Conway's proof of Morley's Theorem

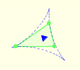
In this page you can play with an interactive animation about John Conway's proof of Morley's Theorem.

The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle (Morley's triangle)

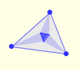
This was a surprising discovery made by Frank Morley (1899).

Conway wrote: "Morley's theorem is renowned as being a theorem that's really hard to prove. Very simple to state, but very hard to prove." (John Conway).

His proof is considered the simplest and a very good example of a "backward proof".

"We can prove Morley's theorem simply as follows. First, please tell me the three angles A, B, C, of your original triangle. Remember they have to add up to 180 degrees. Here's the plan. I'm going to start from an equilateral triangle of some size

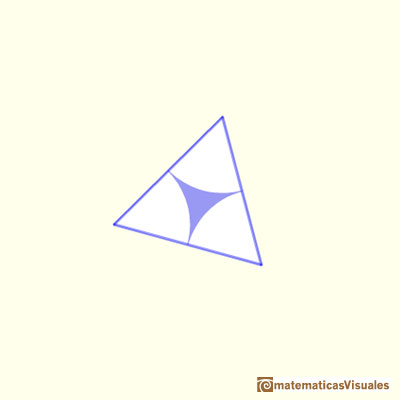
Conway's proof of Morley's Theorem: start from an equilateral triangle of some size | matematicasVisuales

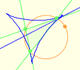
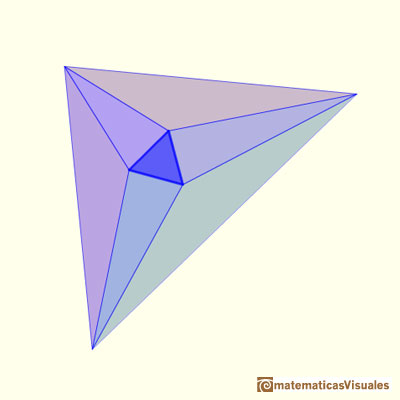
and build up six other triangles around it, and glue them together to create a triangle that has angles A, B and C, just like yours; so for some choice of the size of the equilateral triangle, my construction will exactly reproduce your original triangle; furthemore the method of construction will prove that if you trisect your triangle's angles, you'll find muy equilateral triangle in the middle. Here are the six triangular pieces that we will build around the equilateral triangle." (John Conway)

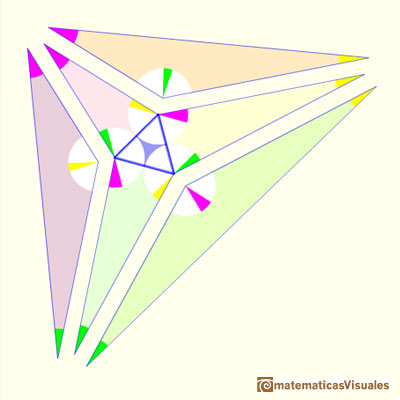
Conway's proof of Morley's Theorem: Here are the six triangular pieces that we will build around the equilateral triangle | matematicasVisuales

"To understand the proof correctly, you must think of the six new triangles as pieces that we are going to define, starting from equilateral triangle, with the help of the values A, B and C that you supplied. The previous figure is our destination, not our starting point.

We construct the six new triangles by first defining their shapes, then defining their sizes. To define the shapes of the six triangles, we fix their angles. " (John Conway)

White angles are 60 degrees angles. You can check that the angles in each triangle sum to 180.

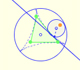
Shapes of the first three triangles:

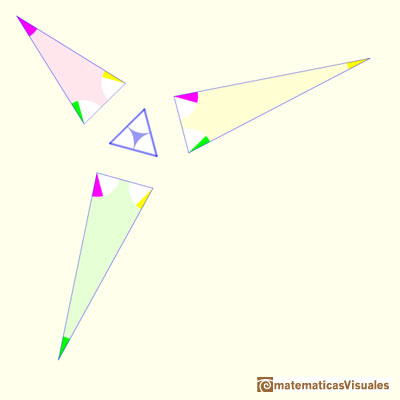
Conway's proof of Morley's Theorem: You can check that the angles in each triangle sum to 180 | matematicasVisuales

To fix the sizes of these three triangles we make the length of one side equal to the equilateral.

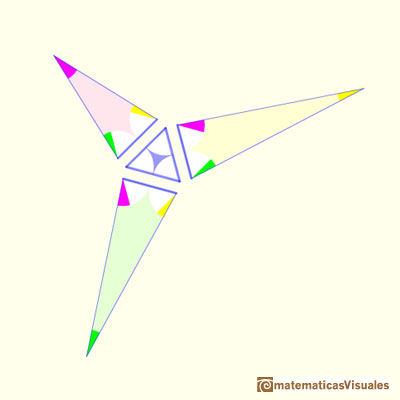
Conway's proof of Morley's Theorem: Fixing sizes | matematicasVisuales

We can glue these three triangles to the equilateral triangle:

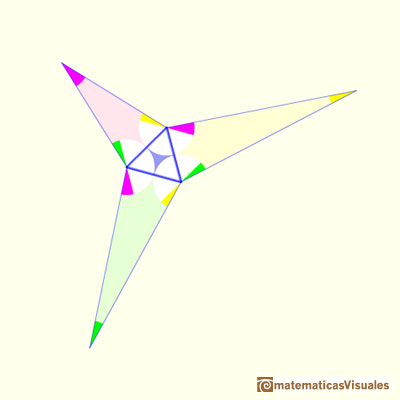
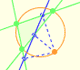
To fix the sizes of the three obtuse triangles we introduce two lines that meet the long side of each triangle ("a bit like dropping perpendiculars", wrote Conway). These lines forms isosceles triangles.

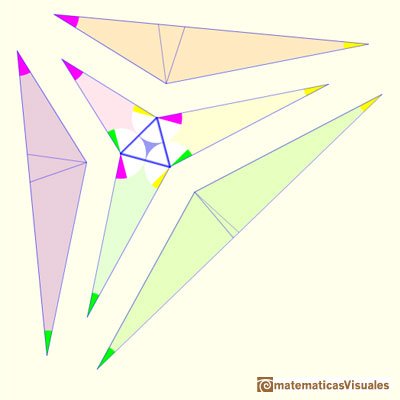
Conway's proof of Morley's Theorem: we introduce two lines that meet the long side of each triangle (a bit like dropping perpendiculars, wrote Conway) | matematicasVisuales

We can fix the size of these triangles so that these lines have the same length as the side of th equilateral triangle.

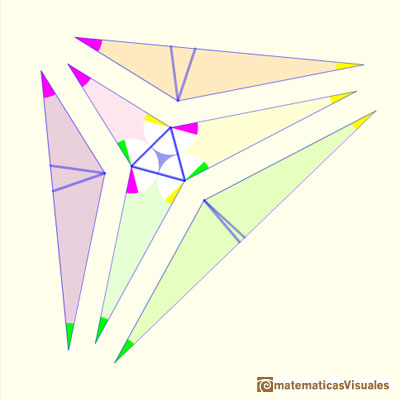
But, how we can draw these lines? Look at the figures to understand the angles.

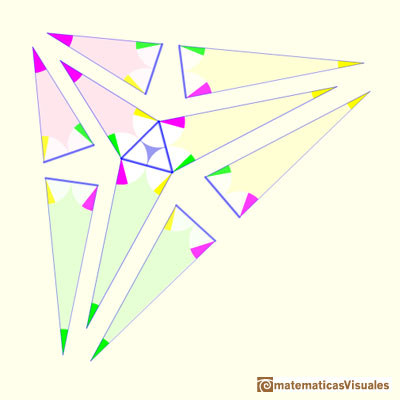
Conway's proof of Morley's Theorem: isosceles triangles | matematicasVisuales

Three triangles with the same color are identical (perhaps one is a mirror image of the other). They have three identical angles and one identical side (equal to the equilateral's side).

Conway's proof of Morley's Theorem: equal triangles | matematicasVisuales

Now we have to check the measure of the angles and that the angles around any one internal vertex sum to 360 degrees.

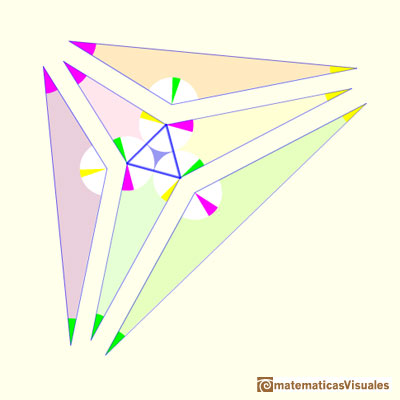
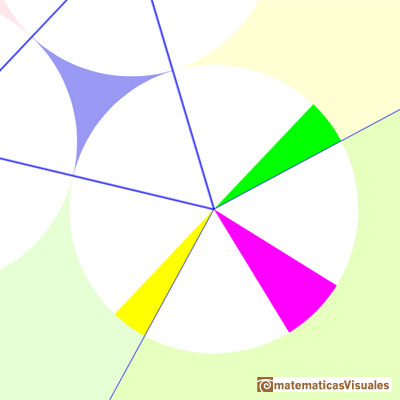
Conway's proof of Morley's Theorem: Checking angles | matematicasVisuales

"Thus, gluing the seven pieces together, I've made a triangle with your angles, for witch Morley's theorem is true.

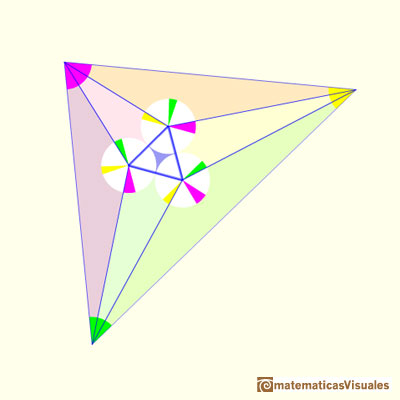
Conway's proof of Morley's Theorem: Gluing triangles | matematicasVisuales

Therefore, Morley's theorem is true for your triangle, and for any triangle you could have chosen". (John Conway)

Conway's proof of Morley's Theorem: The theorem is true | matematicasVisuales

Conway's proof of Morley's Theorem: The theorem is true for any triangle | matematicasVisuales

REFERENCES

John Conway. On Morley's Trisector Theorem, The Mathematical Intelligencer, 2014.

John Conway. The Power of Mathematics.

Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer.

Coxeter, H. S. M. Introduction to Geometry, 2nd ed. New York: John Wiley and sons, 1969.

next NEXT

The deltoid and the Morley triangle

Steiner Deltoid and the Morley triangle are related.

Morley Theorem

The three points of intersection of the adjacent trisectors of the angles of any triangle are the vertices of an equilateral triangle (Morley's triangle)