The Tetraxis^® toy is a geometric puzzle. It is made of twelve identical pieces. Several magnets help guide and hold the pieces together and it is a puzzle not difficult to solve and a real pleasure. It is not difficult to build one using cardboard and some magnets or a 3D printer.

It was designed by Jane and John Kostick. You can see more of their wonderful work (in metal and wood) in Jane and John Kostick's website.

Tetraxis^® is a registered trademark of KO Sticks LLC.

On this page we are going to study some of its properties, in particular, the relation between the Tetraxis^® toy and the rhombic dodecahedron, the shape of the hollow space surrounded by the twelve pieces of the puzzle, which you can build by downloading a template.

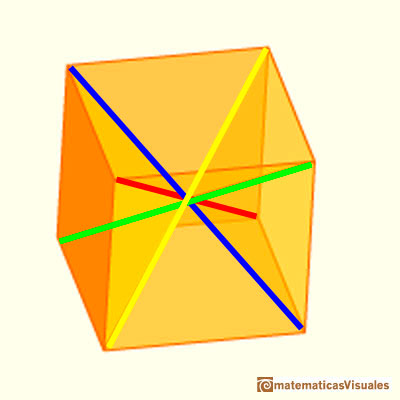
The name Tetraxis^® means four axis. The Greek prefix 'tetra' means 'four' (as in 'tetrahedron', four faces). This is because the twelve pieces of this puzzle line up along four axes.

These four axes are related to the cube. The twelve pieces line up in the directions of the four long diagonals of a cube.

We also encounter these long diagonals when studying a polyhedron discovered by Johannes Kepler: the rhombic dodecahedron.

A rhombic dodecahedron is a polyhedron that has twelve rhombic faces. It can be seen as a cube capped with six pyramids:

The rhombic dodecahedron has wonderful properties. It tessellates space in a way that is related to how bees build their honeycombs. It has vertices of two different kinds: four edges met in six of these vertices of three edges met in eight vertices of the rhombic dodecahedron.

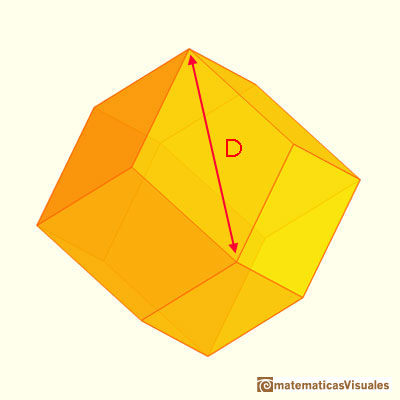
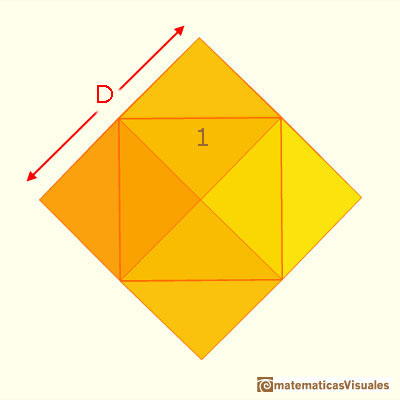
Studying the relationships between the Tetraxis^® toy and the rhombic dodecahedron it is interesting to pointing out the ratio between the two diagonals of the rhombic faces of this polyhedron.

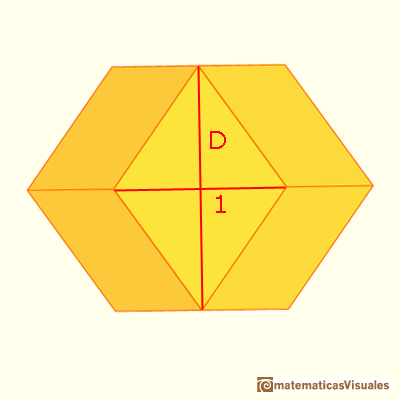
We could calculate the diagonal D of one of these rhombuses:

These rhombuses are related with the proportions of the standard size of paper DinA.

Standard Paper Size DIN A

There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.

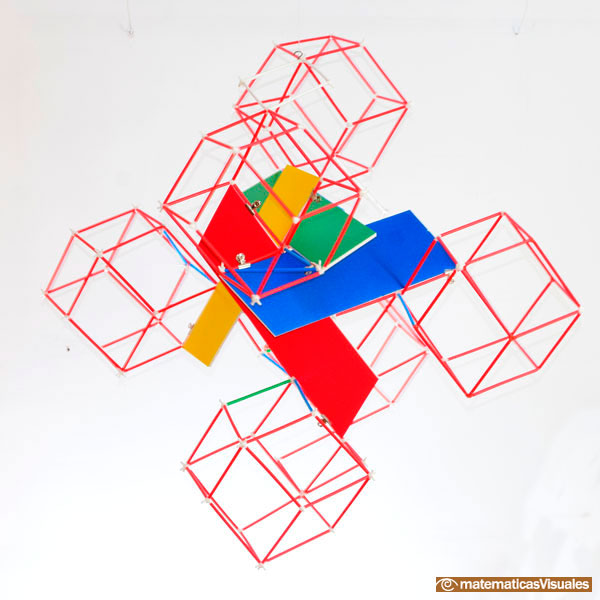
I built this model to have a better understanding of Tetraxis^®. It is made up several rhombic dodecahedra:

This structure is inspired in this beautiful video.

These are the four directions on a rhombic dodecahedron:

You can build a Tetraxis^® using cardboard. Some magnets inside hold the pieces together. Neodymium magnets are perfect but they could be dangerous for children (in particular, if they eat them).

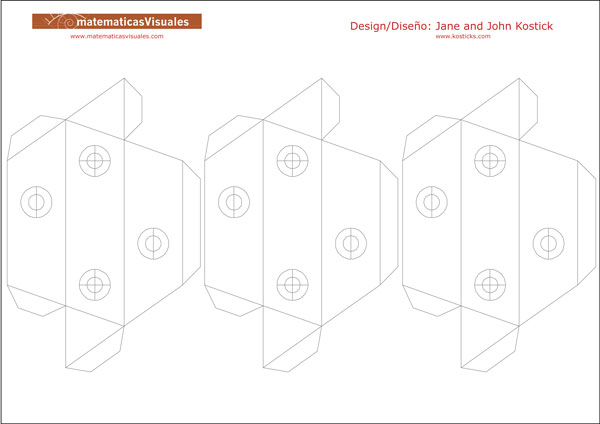
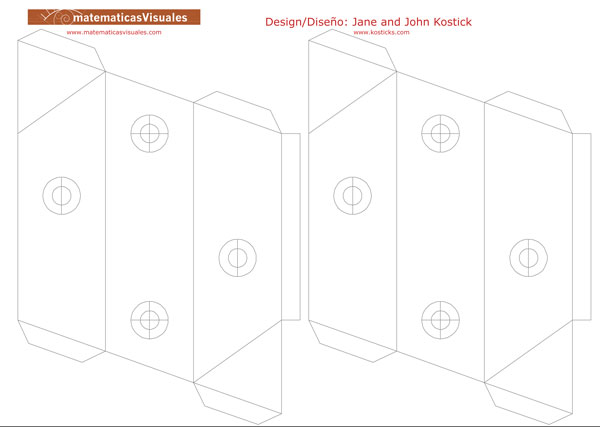
You could download this template, print it on cardboard, cut, fold and glue it to build the shape of a Tetraxis^® stick. We need twelve pieces and we can use four different colors.

Circles indicate the location of the magnets. You can glue four magnets (notice the two different polarities). I used two neodymium magnets and two pieces of metal. Magnets and pieces of metal will remain inside the stick.

As an alternative, using the following model you can build a smaller Tetraxis^®. I think that the big one is much better!

This is the result. A wonderful puzzle, easy to build and a pleasure to solve it.

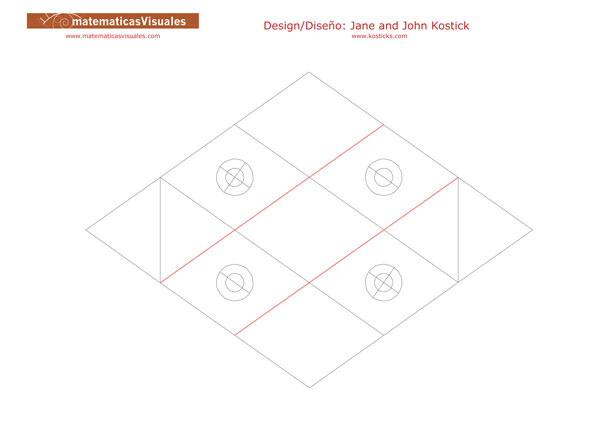
There is another different way to draw the plane net of the pieces of the Tetraxis^® puzzle. The following template is inspired by an original drawing by Jane Kostick:

Nine small rhombuses make a similar big rhombus that is the exterior shape of each piece. Four magnets are at the centers of four of the smaller rhombuses.

The diagonals of these rhombuses are in the ratio square root of two.

More about the geometry of the Tetraxis in Kosticks web site.

Another way to build a Tetraxis^® is using a 3D printer.

In the following photo we can see how the four colors meet in some places.

There are six of this combinations of four pieces. These are related with the six faces of a cube or the six vertices of a rhombic dodecahedron where four edges met.

In the following photo we see a combination of three pieces that is like a bow tie. There are twelve of these, one for each piece of the puzzle. Each of them is related to one face of a rhombic dodecahedron or to one edge of a cube.

There are eight combinations of three colors like the following one. Each is related with the vertices of a cube or the eight vertices of a rhombic dodecahedron where three edges met.

More about these combinatorial properties of the Tetraxis in Koskticks web site.

The shape of the hollow space inside an assembled Tetraxis^® toy is a rhombic dodecahedron.

A beautiful video about the Tetraxis and the rhombic dodecahedron: Dissecting a Rhombic Dodecahedron with Miles.

MORE LINKS

Rhombic Dodecahedron (1): honeycombs

Humankind has always been fascinated by how bees build their honeycombs. Kepler related honeycombs with a polyhedron called Rhombic Dodecahedron.

Kepler, cannonballs and Rhombic Dodecahedron.

Kepler understood that the Rhombic Dodecahedron is related with the optimal sphere packing. If a precise structure of balls is squeezed we get rhombic dodecahedra.

The volume of a cuboctahedron

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of a cube.

The volume of a cuboctahedron (II)

A cuboctahedron is an Archimedean solid. It can be seen as made by cutting off the corners of an octahedron.

Leonardo da Vinci: Drawing of a cuboctahedron made to Luca Pacioli's De divina proportione.

Leonardo da Vinci made several drawings of polyhedra for Luca Pacioli's book 'De divina proportione'. Here we can see an adaptation of the cuboctahedron.

Stellated cuboctahedron

The compound polyhedron of a cube and an octahedron is an stellated cuboctahedron.It is the same to say that the cuboctahedron is the solid common to the cube and the octahedron in this polyhedron.

Rhombic Dodecahedron (2): honeycomb minima property

We want to close a hexagonal prism as bees do, using three rhombi. Then, which is the shape of these three rhombi that closes the prism with the minimum surface area?.

Rhombic Dodecahedron (3): Augmented cube

Adding six pyramids to a cube you can build new polyhedra with twenty four triangular faces. For specific pyramids you get a Rhombic Dodecahedron that has twelve rhombic faces.

Rhombic Dodecahedron (4): Rhombic Dodecahedron made of a cube and six sixth of a cube

You can build a Rhombic Dodecahedron adding six pyramids to a cube. This fact has several interesting consequences.

Rhombic Dodecahedron (6): A Rhombic Dodecahedron inside and outside a cube

A chain of six pyramids can be turned inwards to form a cube or turned outwards, placed over another cube to form the rhombic dodecahedron.

Rhombic Dodecahedron (5): Rhombic Dodecahedron is a space filling polyhedron

The Rhombic Dodecahedron fills the space without gaps.

Rhombic Dodecahedron (7): Maraldi angle

The obtuse angle of a rhombic face of a Rhombic Dodecahedron is known as Maraldi angle. We need only basic trigonometry to calculate it.

Trapezo-Rhombic Dodecahedron

There are two essential different ways to pack spheres in an optimal disposition. One is related with the Rhombic Dodecaedron and the other to a polyhedron called Trapezo-rombic dodecahedron..

Standard Paper Size DIN A

There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.

Volume of an octahedron

The volume of an octahedron is four times the volume of a tetrahedron. It is easy to calculate and then we can get the volume of a tetrahedron.

Chamfered Cube

You can chamfer a cube and then you get a polyhedron similar (but not equal) to a truncated octahedron. You can get also a rhombic dodecahedron.