Geometric sequences or geometric progressions
A sequence is an ordered list of numbers. Some sequences follow a pattern.
Each number in a sequence is called a term.
If we see the sequence as a function, its domain is the natural numbers.
A Geometric sequence (or geometric progression) is a sequence of numbers where each term after the first is given by multiplying the previous one by a fixed non-zero number, a constant, called the common ratio.
Any term of a geometric sequence can be expressed by the formula for the general term:

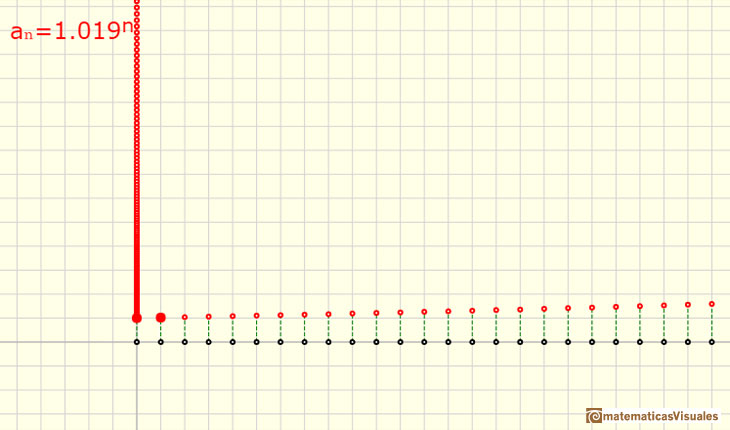
When the ratio r is greater than 1 we have an increasing sequence (expontential growth).
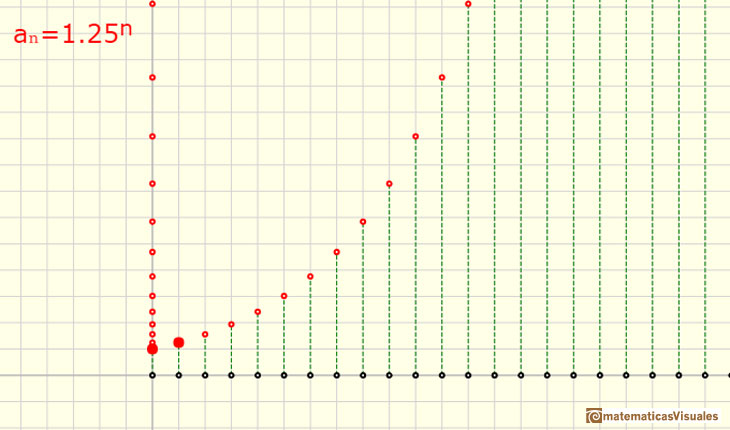
Even if the ratio is very small the sequence starts increasing slowly but after enough steps the growth becomes bigger and bigger. For example, this is the result after 300 steps if the ratio is 1.01:
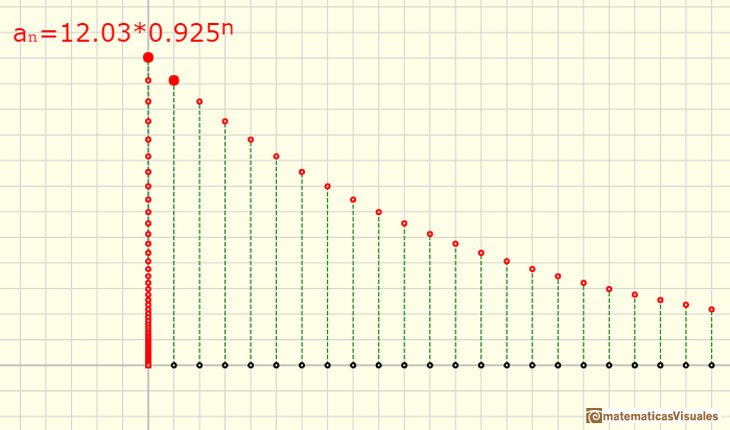
If the ratio r is positive and less than 1 the sequence is decreasing and the general term tends towards 0.
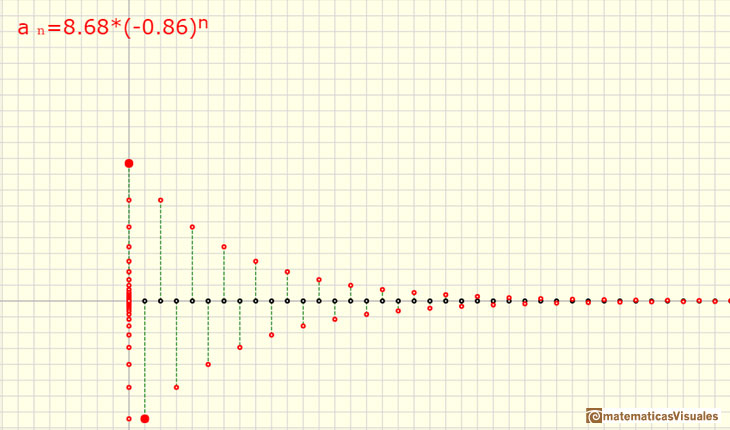
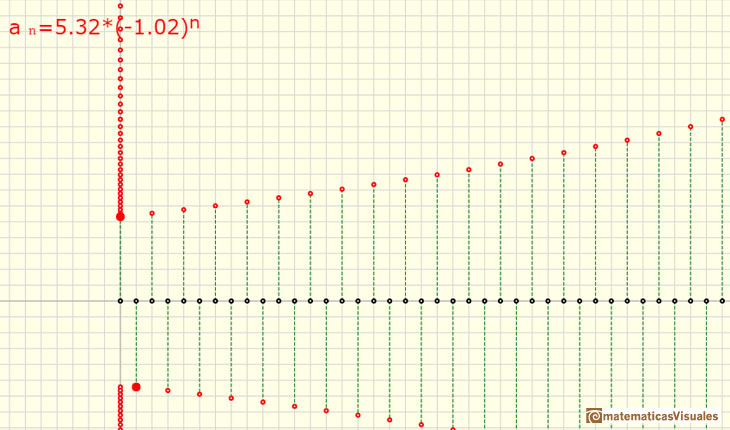
When the ratio r is negative the sequence is alternating.
If the ratio r is between -1 and 0 the alternating sequence has a general term that tends towards 0.
If the ratio r is less than -1 the alternating sequence in absolute value tends towards infinity (unsigned if we consider the value, due to the alternating sign).
We can consider the sum of the n terms of a geometric sequence.
We can deduce a formula:
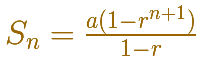
In the next application we can play with different cases with a positive common ratio:
You can see the behavior if the common ratio is greater than 1 (the sum grows and grows):
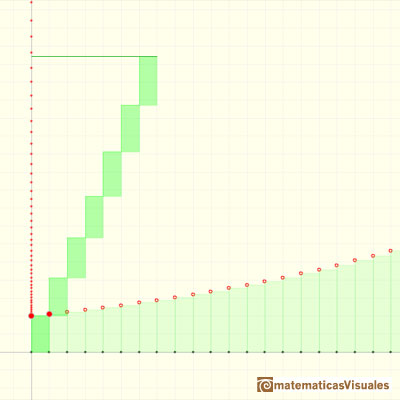
If the common ratio is less than 1 the sum seems to approach a number:
A series is the sum of the infinite terms of a sequence.
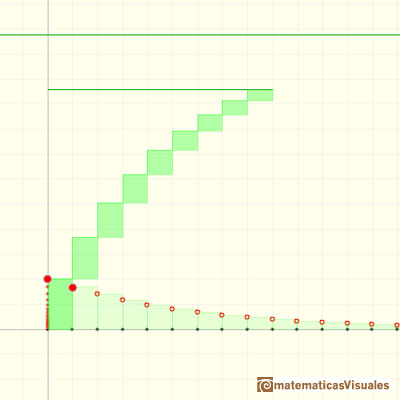
If a positive r is less than 1 you can sum up these infinite numbers and the result is a number. We can say that the series is convergent (it approaches some limit).
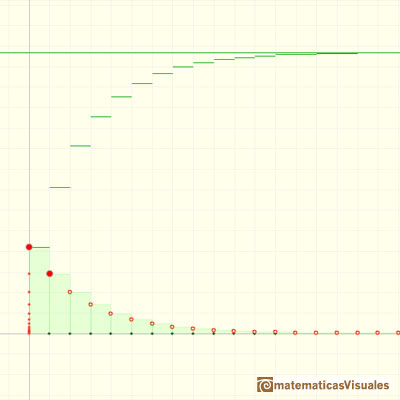
If a positive r is greater or equal to 1 then the series do not approaches some number because it becomes bigger and bigger. Then we can say that the series is divergent.
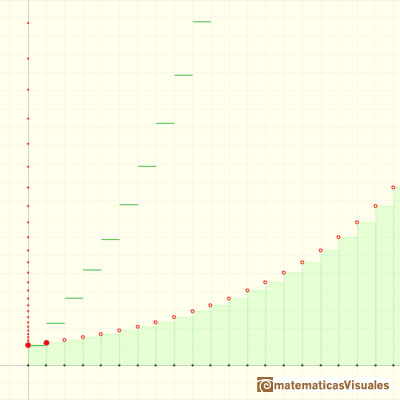
In the next application we can play with a general case. Now the common ration can be positive or negative:
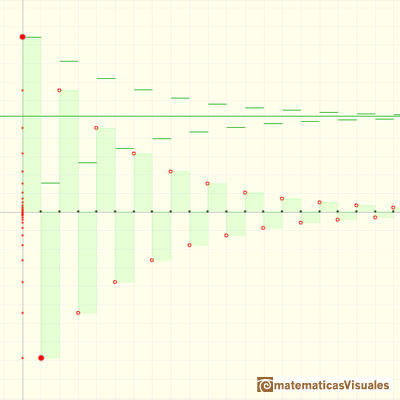
A divergent alternatig series:
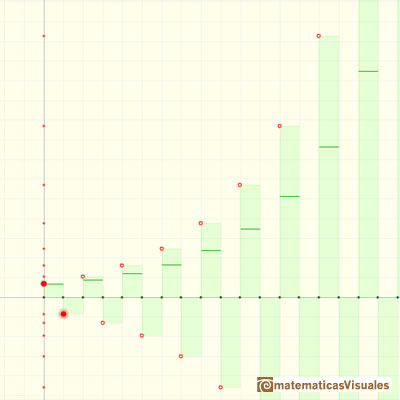
A convergent alternatig series:
The condition for the convergence of a geometric series with a non-zero common ratio r is:
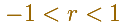
And the formula is:
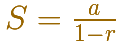
 NEXT
NEXT
MORE LINKS

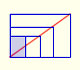
The geometric series of ratio 1/2 is convergent. We can represent this series using a rectangle and cut it in half successively. Here we use a rectangle such us all rectangles are similar.
We can study several properties of exponential functions, their derivatives and an introduction to the number e.
Using a decreasing positive function you can define series. The integral test is a tool to decide if a series converges o diverges. If a series converges, the integral test provide us lower and upper bounds.
The integral of power functions was know by Cavalieri from n=1 to n=9. Fermat was able to solve this problem using geometric progressions.
There is a standarization of the size of the paper that is called DIN A. Successive paper sizes in the series A1, A2, A3, A4, and so forth, are defined by halving the preceding paper size along the larger dimension.