


Hemos visto en una entrada anterior que podemos decir que todos los cuadrados son semejantes y que hay relación entre la diagonal y el lado de un cuadrado.

De momento, no hemos hecho cuentas. Esas vendrán enseguida.
También hemos visto que si dividimos una entre otra, por ejemplo, la diagonal dividido entre el lado, siempre obtenemos el mismo número, es decir, que es una constante, que es igual para todos los cuadrados.
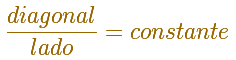
Y lo hemos escrito de un modo más abstracto:

Decimos que ese número constante es 'la RAZÖN entre la diagonal y el lado de un cuadrado'.
Luego hemos empezado a usar un lenguaje para expresar esta relación que es el lenguaje de las funciones:
Podemos decir que la longitud de la diagonal 'DEPENDE' del lado. Cuando usamos esa expresión lo que hemos hecho ha sido elegir el lado como 'VARIABLE INDEPENDIENTE' y la diagonal como 'VARIABLE DEPENDIENTE, porque depende del lado. Podemos decir que nosotros podemos modificar el lado y conforme hagamos eso irá cambiando la diagonal, que 'DEPENDE' del lado.
Ahora vamos a profundizar un poco más en este lenguaje de las funciones.
Para escribir que la diagonal depende del lado usamos paréntesis:
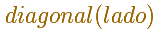
Si lo escribimos más compacto podemos poner:
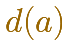
para expresar 'la diagonal de un cuadrado de lado a'.
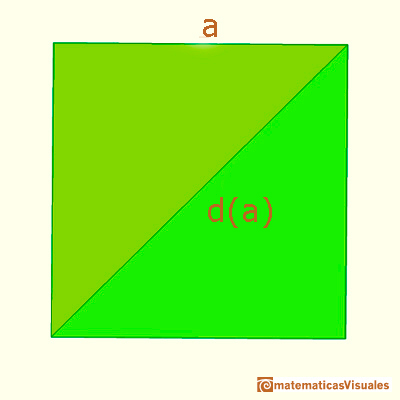
Mira como escribiremos la diagonal de un cuadrado de lado 1:
La diagonal de un cuadrado de lado 2:
La diagonal de un cuadrado de lado doce y medio:
Así expresamos una frase muy importante:
La RAZÓN (la división) entre la diagonal de un cuadrado y su lado a es constante, no depende de lo grande o pequeño que sea el cuadrado.
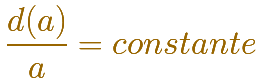
Es decir, que si tenemos cuadrados de lado a, lado b, lado 1, lado 2 ... podemos escribir
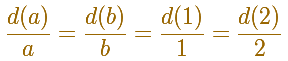
Pero fíjate que hemos escrito esto que debemos simplificar
Por lo tanto, escribiremos
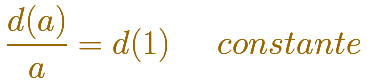
Despejamos, llegamos a una relación interesante, que parece complicada pero ya verás que no lo es tanto:
Es una manera abstracta, por lo tanto dificil pero útil, de escribir frases que nos resultan familiares. Vamos a verlo:
La diagonal de un cuadrado que tiene un lado que mide 2 es el doble de la de un cuadrado que tiene de lado 1:
La diagonal de un cuadrado que tiene un lado que mide 3 es el triple de la de un cuadrado que tiene de lado 1:
Hasta podríamos escribir (pero esto ya es muy dificil):
Lo que queremos expresar es que si tenemos un cuadrado cuyo lado mide a y multiplicamos ese lado por un número positivo k, entonces la diagonal la hemos multiplicado también por k.
Esta página es más dificil de lo que parece. Por eso, quizás tengamos que leerla varias veces para comprenderla. Estamos usando un lenguaje complicado pero muy útil que es el lenguaje de las FUNCIONES.
Además hemos aprendido que para calcular la diagonal de un cuadrado basta con saberla calcular para un solo caso. ¡Es suficiente hacerlo UNA SOLA VEZ EN LA VIDA!
Y ese caso lo podemos elegir todo lo SENCILLO que queramos. Por ejemplo, podemos calcular la diagonal de un cuadrado de lado 1.
Eso es lo que podemos hacer a continuación. Unas cuentas, que es tarea más concreta y nos resultará más fácil.
Usando el teorema de Pitágoras, calcularemos la relación que hay entre la diagonal y el lado de un cuadrado.
 ANTERIOR
ANTERIOR
MÁS ENLACES













